Functional Programming

Shortcut to this page: ntrllog.netlify.app/fp

Notes provided by Professor John Hurley (CSULA)

(all code examples are done in Kotlin with expression bodies when possible)

Pure Functions

A pure function is a function that:

• always returns the same value for the same input
• has no side effects

Referential Transparency

Consider the function:

and consider the input `n=3`. We can see that for `n=3`, the output will always be `6` no matter what.

This can be thought of as referential transparency, meaning that calls to the same function with the same arguments will always return the same value.

That's Not Very Referentially Transparent of You

An example of a function that's not referentially transparent is this:

If the value of cost is changed, then getCost() will return something different for the same input.

Side Effects

Side effects are changes that are caused by a function call, but the changes themselves occur outside of the function call. These changes usually are not necessary for calculating the return value of the function (assuming, in the spirit of functional programming, that the primary purpose of a function is to return something rather than do something). Some examples of side effects are:

• modifying a variable beyond the scope of the block where the change occurs
• modifying a data structure in place
• setting a field on an object
• throwing an exception or halting with an error
• printing to the console
• reading user input
• reading from or writing to a file
• drawing on the screen

This is an example of a function that modifies a variable outside of its scope (and prints):

Data Immutability

In functional programming, data are not allowed to be changed* once it is created. So something as simple (and seemingly essential) as a loop is not allowed. Consider this loop:

num and squaredNums are being changed on every iteration of the loop, and data are not allowed to be changed!

*Changed means reassigned to a different value.

Instead of loops, recursion is used.

In the context of lists, if we want a different list (e.g., one of the elements need to be changed or removed), then we need to create a new list instead of modifying the original list.

Why Functional Programming?

With functional programming, there are no side effects; there are no mutable data; and there is referential transparency. All of these make functional programming great for concurrent programming because there is no shared state, data synchronization issues, race conditions, and deadlocks.

The code is more modular since there is no shared state.

Pure functions are less buggy than impure functions. Since they don't depend on external state, pure functions are more reliable once they are thoroughly tested. Pure functions also don't have side effects, so they don't create unpredictable problems.

Referential transparency makes it possible to cache the result of a function call, so that the result can be used instead of calling the function again. (This is called memoization.)

Tail Recursion

Whenever a function call is made, a stack is created for that function call. So for recursive functions, a stack is created for each recursive call.

If too many recursive calls are made, then too many stacks will be created, resulting in a stack overflow. Since we're pretty much limited to recursion in functional programming, we have to find a way to use recursion without running into a stack overflow.

Well, we can avoid having too many stacks by getting rid of them once we don't need them anymore. Going back to the recursion animation above, notice that each stack after the main stack needs to allocate memory for an Int (the n in n * factorial(n-1)). This means that the recursive call is not the last thing that is performed in the stack (the multiplication is the last thing being performed). Because we need to store the n in each stack in order for the recursion to work, we cannot simply remove the stack after a recursive call. But it would be nice to be able to do so!

So if we don't want to store anything in each stack, then that means we should push all the information we need to the next stack. Consider this modified factorial function:

This modification pushes the result of each multiplication forward (in the accumulator) so that it doesn't need to be stored.

(lol there's no animation here.)

Notice now that the recursive call is the last thing that is performed in the stack and that no memory needs to be allocated to store anything — this is tail recursion! Capable compilers are able to take advantage of this and remove the previous stack on each recursive call — after all, there's no important information being stored in the previous stack (this is tail-call elimination/optimization!)

The fact that the stacks can be removed is nice, but this factorial function is a bit awkward. It's not intuitive to need two parameters to calculate the factorial of a number. In addition, if we accidentally put the wrong initial value for the accumulator, then the answer will be wrong.

Helper Function to the Rescue!

Consider this final version of the factorial function:

Here, we have a nested function (helper()) that is called recursively. The outer function (factorial()) is no longer called recursively; instead it kicks off the recursive process. This allows the factorial function to be clean while still getting the benefits of tail-call elimination.

A Systematic Approach to Making Functions Tail Recursive

There are three main ideas:

• there is an outer function that defines and calls an inner function, which is going to be the recursive one
• the inner function takes in an accumulator that starts with an initial value and builds up the result at each recursive step
• the base case returns the accumulator

Let's look at string reversal as an example.

There is an outer function:

That defines an inner function, which takes in an accumulator:

The base case returns the accumulator:

The inner function is recursive and the accumulator builds up the result at each recursive step:

The outer function calls the inner function with an initial value for the accumulator:

Currying

Currying is taking a function with multiple arguments and breaking it up into mutiple functions, each with one argument.

(I feel like a function that adds two numbers is a very contrived and overused example, but let's roll with it!) Suppose we have a function that adds two numbers:

Now suppose we have a use case where we always want to add `5` to any number. Of course, we can simply just do myAdd(x, 5), whenever we need to, but we can make the function calls simpler and clearer. The idea is to create a new function (let's call it addFive()) that takes in only one argument and adds `5` to it. Simpler and clearer.

Time to curry the myAdd() function!

We broke the myAdd() function into two smaller functions, each with one argument. The outer function takes in one of the arguments (x) and simply returns another function. That other function takes in the other argument (y) and does what the original myAdd() function would've done. Since the outer function returns a function, we can create new functions, like add5().

Let's look at a more complicated, but more practical, example. Suppose we had our own filter function that filtered a list based on a custom function:

Time to curry!

With this example, we can see a more useful reason to use currying. Imagine if we wanted to create filterEven() and filterOdd() but without currying.

Notice how they're almost exactly the same. It seems like wasted repetition to create two similarly-defined functions this way.

Polymorphic Functions

Consider this function that searches for a string in a list of strings:

This is a monomorphic function because it operates only on one type of data, namely strings.

What if we wanted to search for an integer in a list of integers?

With the exception of the parameter types, the code is exactly the same. Of course, it seems like a waste to create two separate functions that do the exact same thing, just with different types.

Polymorphic functions are functions that operate on any type that it is given.

This function will work for strings, ints, doubles, anything really.

Here's a pretty cool example of quicksort with generic types and a predicate function:

As convenient as it looks, we don't always want polymorphic functions to accept any type. To show why, here's a simple example:

Obviously, this only works with number-like types; so if we pass in a string, things will go wrong. To prevent this, we can restrict the types that can be used as type arguments:

This says that we can pass in any type for A as long as it is a Number type.

A more practical example would be writing one compare function that works for multiple types, including custom classes:

Here, we can pass in any type for A as long as it is Comparable.

Generics

This naturally leads us to the concept of subtypes and supertypes. Suppose we have two types, `A` and `B`. Type `B` is a subtype of type `A` if you can use type `B` whenever type `A` is required. For example, Int is a subtype of Number; whenever the code expects a Number, we can pass an Int because technically, an Int is a Number.

To be a little more precise, in order for a type to be a true subtype (i.e., in order to fit the actual definition of what it means to be a subtype), we must be able to replace the supertype with the subtype without causing any errors. This means that:

• A subtype must accept all argument types that the supertype can accept
• A subtype must not return a result type that the supertype won't return

(When I say subtype and supertype here, I mean their functions.)

(The following illustrations are adapted from https://typealias.com/guides/illustrated-guide-covariance-contravariance/. Most of the information in this section is also from that website.)

For example, suppose we had a supertype with a function that takes in a shape and returns a color. It only accepts one square or one circle and returns only green or blue.

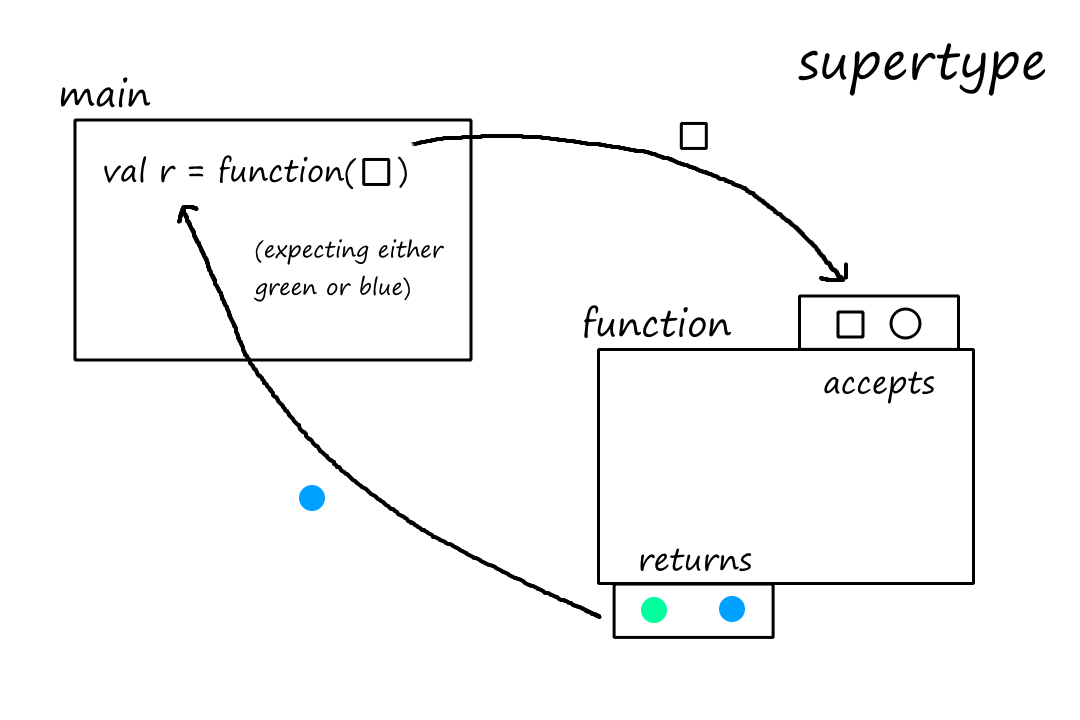
In order for a type to be a true subtype of the supertype, we have to be able to replace the supertype with the subtype without causing errors. The first rule says that "a subtype must accept all argument types that the supertype can accept". Let's see what happens if we don't follow that rule, i.e., the subtype does not accept all argument types that the supertype can accept.

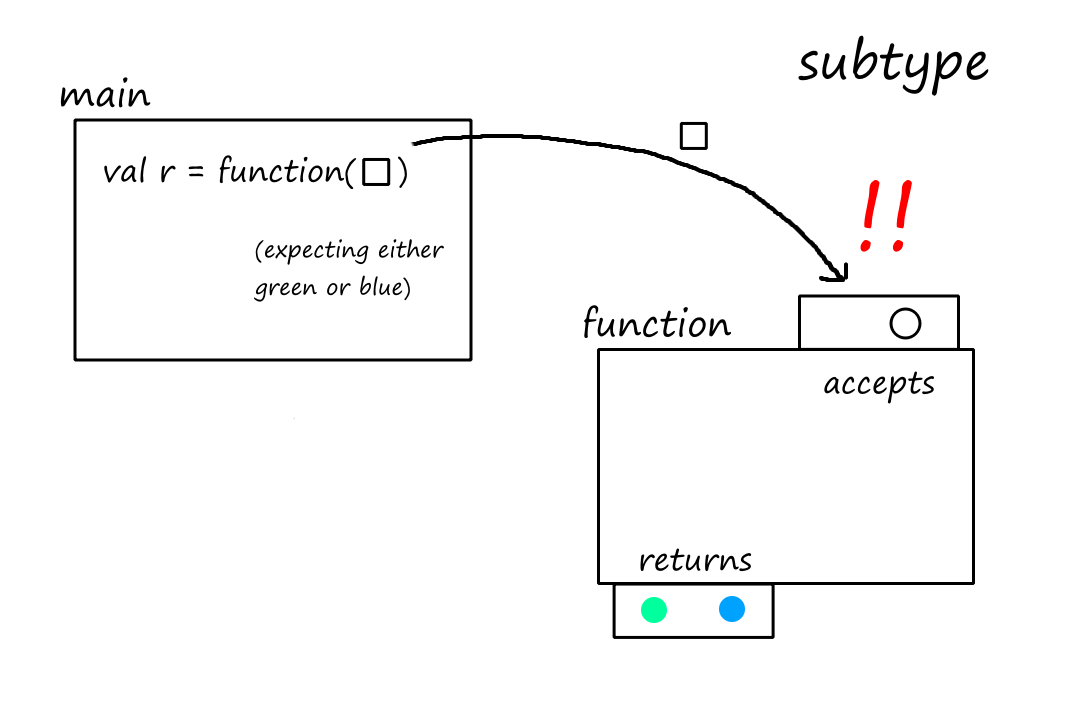
In this case, the subtype only accepts circles. The supertype accepted squares, and the function call in main was expecting the code to work with passing in a square. But when we replaced the supertype with the subtype, the code broke. So the subtype is not a true subtype.

Let's look at the second rule: "a subtype must not return a result type that the supertype won't return". Again, we'll see what happens when we don't follow that rule, i.e., the subtype does return a type that the supertype doesn't return.

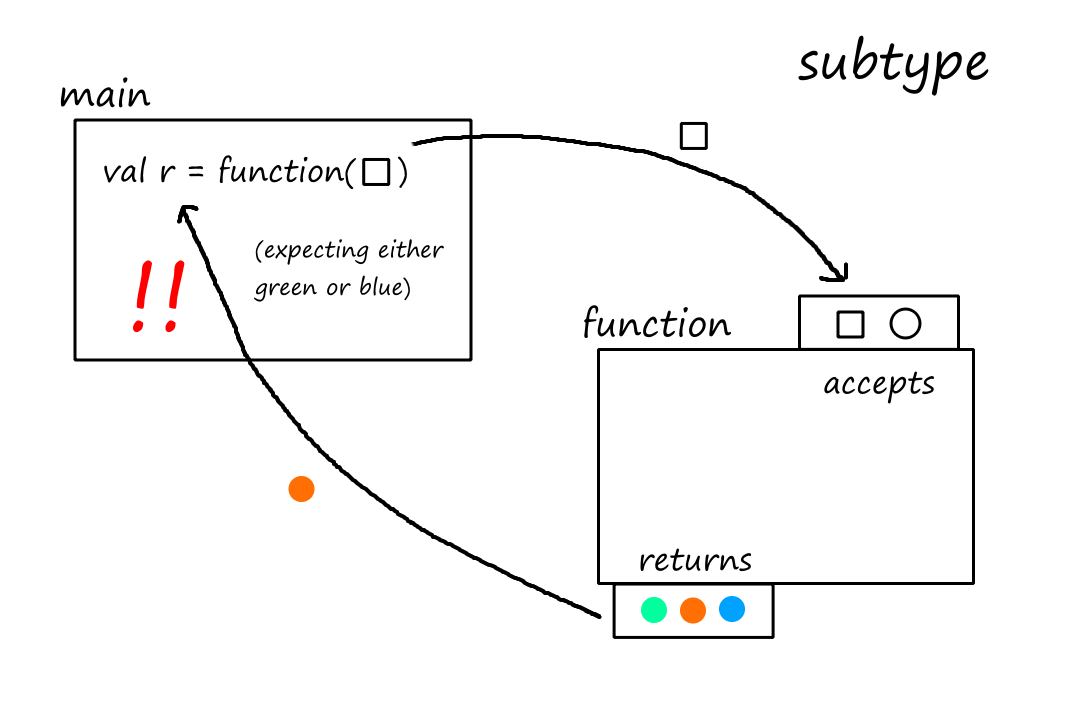
This time, the subtype can also return orange. The supertype only returned green or blue, and the function call in main was expecting only green or blue, not orange! So the subtype is not a true subtype.

Now, this doesn't mean that if we want to create true subtypes, we have to create carbon copies of the supertype. (If this was the case, there wouldn't really be a point in creating subtypes in the first place.) Subtypes can be a little bit more flexible and still be a true subtype.

Contravariance

Let's change the first rule from "a subtype must accept all argument types that the supertype can accept" to "a subtype must accept at least the argument types that the supertype can accept". Under this new rule, the subtype still technically accepts "all" the argument types that the supertype can accept, just a little bit more.

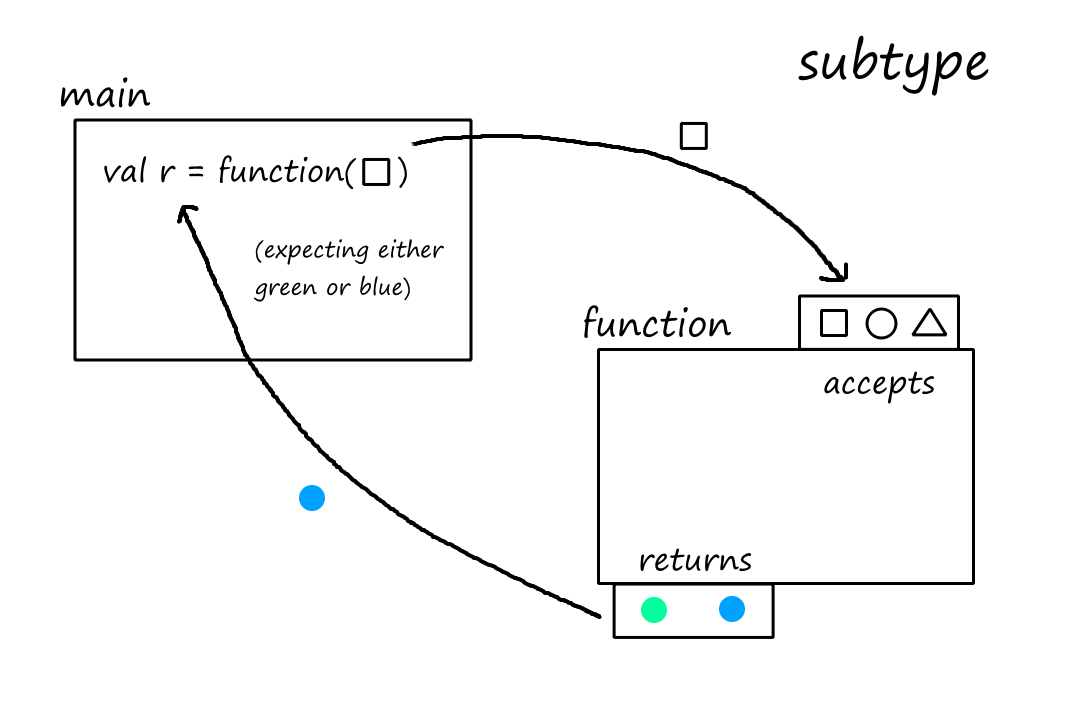
And this is fine. Remember that the definition of a true subtype is that we can replace the supertype without causing any errors. As far as main is concerned, it is still interacting with the supertype, so main will continue to pass only squares and circles.

This is called contravariance because as the type gets more specific ("narrower"), the type of arguments that can be accepted get more general ("expands"). They go in opposite directions, hence the "contra".

Covariance

Let's change the second rule from "a subtype must not return a result type that the supertype won't return" to "a subtype must return at most the same result types that the supertype returns". Under this new rule, the subtype can choose to exclude something the supertype returns.

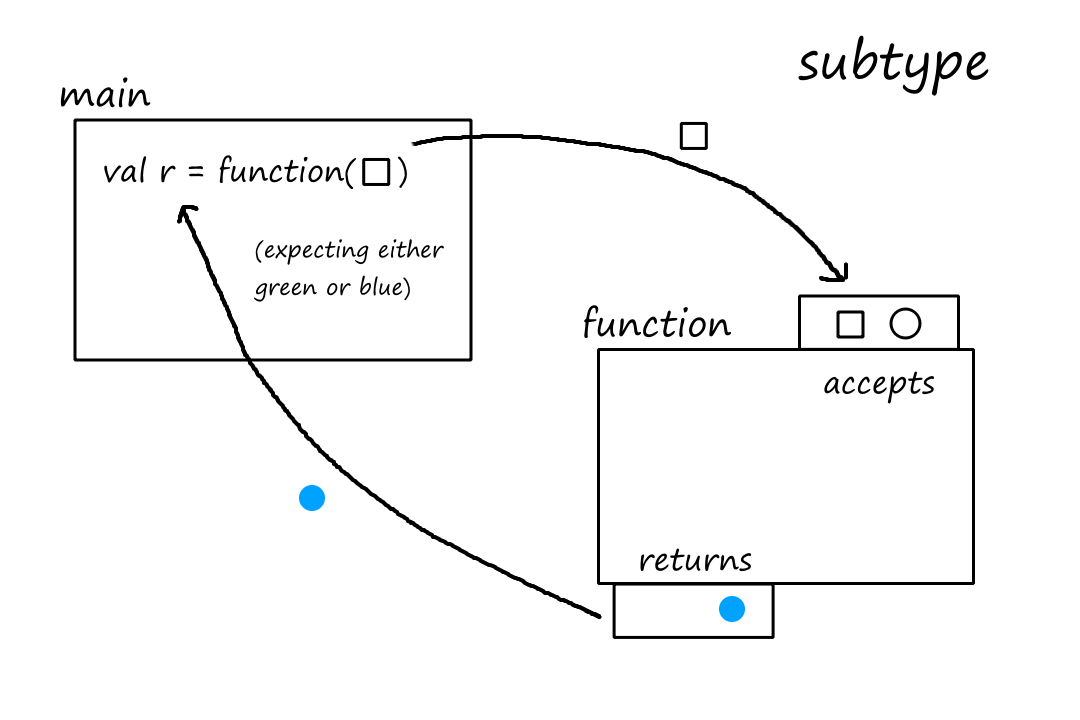
Again, this is fine because main is expecting either green or blue.

This is called covariance because as the type gets more specific ("narrower"), the return types also get narrower. They go in the same direction, hence the "co".

New Rules!

So now the two rules for a subtype to be a true subtype are:

• A subtype must accept at least the argument types that the supertype can accept
• A subtype must return at most the same result types that the supertype returns

Variance

Variance is, at a very basic level, looking at if something is covariant or contravariant (or invariant, which we'll see right now).

Since a String is a subtype of Any, is a MutableList of Strings a subtype of a MutableList of Anys?

This doesn't compile, but if it did, there would be a runtime error when calling the length method on an Int. Since we can't replace a MutableList of Anys with a MutableList of Strings, a MutableList of Strings is not a subtype of a MutableList of Anys.

In fact, MutableList is invariant on the type parameter. That is, for any two different types `A` and `B`, MutableList<A> isn't a subtype or a supertype of MutableList<B>.

Generic Variance (Covariance)

Suppose we have a generic class Group<T>. If `A` is a subtype of `B` and Group<A> is a subtype of Group<B>, then the Group class is covariant. The subtyping is preserved, hence the "co".

Now let's suppose that Group has two functions: insert() and fetch(). (Let's also suppose it's an interface instead of a class just so it compiles.)

Let's say we have two classes: an Animal class and a Dog class, where Dog is a subtype of Animal. If we want to make the Group class covariant, then Group<Dog> should be a subtype of Group<Animal>. Let's see what we have so far and see if it's possible.

Group<Animal> {
    fun insert(item: Animal): Unit
    fun fetch(): Animal
}
Group<Dog> {
    fun insert(item: Dog): Unit
    fun fetch(): Dog
}

The way things are right now, Group<Dog> is not a subtype of Group<Animal> because Group<Dog> does not accept at least the same argument types that Group<Animal> accepts. For example, we could pass in a Cat to Group<Animal>'s insert() function, but we can't pass a Cat to Group<Dog>'s insert() function.

Note that Group<Dog> already returns at most the same result types that Group<Animal> returns, so that rule is not being broken.

Kotlin Variance Annotation (out)

For now, let's remove the insert() function so that the first rule is not broken.

Group<Animal> {
    fun fetch(): Animal
}
Group<Dog> {
    fun fetch(): Dog
}

Since both subtyping rules are not being broken anymore, Group<Dog> is a subtype of Group<Animal>. To tell Kotlin that we want to treat Group<Dog> as a subtype of Group<Animal>, we use the out annotation:

Generic Variance (Contravariance)

On the other hand, if `A` is a subtype of `B` and Group<B> is a subtype of Group<A>, then the Group class is contravariant. The subtyping is reversed, hence the "contra".

If we want to make the Group class contravariant, then Group<Animal> should be a subtype of Group<Dog>. Let's see what we have so far and see if it's possible.

Group<Dog> {
    fun insert(item: Dog): Unit
    fun fetch(): Dog
}
Group<Animal> {
    fun insert(item: Animal): Unit
    fun fetch(): Animal
}

Well, Group<Animal> does accept at least the same argument types as Group<Dog> does, so that rule is fine. However, Group<Animal> can return more types than Group<Dog> can. So the second rule is being broken!

Kotlin Variance Annotation (in)

Similarly to before, let's remove the fetch() function so that the second subtyping rule is not broken.

Group<Dog> {
    fun insert(item: Dog): Unit
}
Group<Animal> {
    fun insert(item: Animal): Unit
}

Now both subtyping rules are not being broken anymore, so Group<Animal> is a subtype of Group<Dog>. To tell Kotlin that we want to treat Group<Animal> as a subtype of Group<Dog>, we use the in annotation:

Abstract Data Types

An abstract data type is a basic (abstract) description of a data structure. It specifies the type of data stored, the operations supported, and the types of parameters of the operations. Most importantly, an ADT specifies what each operation does, but not how the operation does it.

For example, a list is an abstract data type. We can say that the list holds Ints and that the operations we can perform on a list are to insert into and delete from the list. However, we are not specifying how the values of the list are stored, and we are not specifying how the insert and delete operations are implemented.

On the other hand, a linked list is a data structure. Each element in the list is a node that contains a value and a pointer to the next node (we're specifying how the values of the list are stored). Insertion and deletion of elements are performed by following each node's next pointer to traverse the linked list until the desired node is reached (we're specifying how the operations are implemented).

Functional Data Structures

Suppose we wanted to design an interface to compute expressions like `(1+2)+4`.

And to use this to represent `(1+2)+4`, it would look like this:

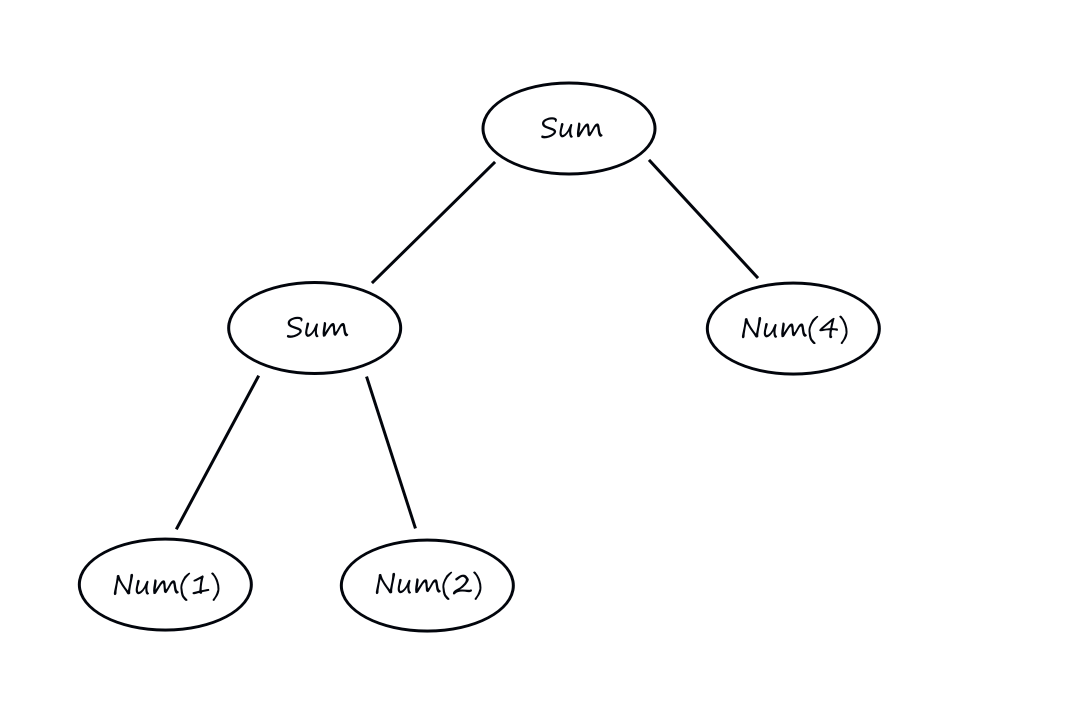
To actually evaluate the result of the expression, we can write a function:

And to call the function:

Recall that in functional programming, data is not modified. This means that functional data structures must be immutable. So we can't use arrays, (imperative) linked lists, etc.

Notice in the Expr example, when evaluating the result of the expression, we never changed any values. We sorta "passed it up the chain".

In principle, if we want to perform insert or delete operations on functional data structures, we make a new copy based on the inputs but with the desired changes, leaving the inputs unmodified.

Singly Linked List

Linked lists are a common functional data structure because

• they're persistent
• prepending (producing a new list) is `O(1)`
• building an `n`-element list is `O(n)`

Here's how a functional singly linked list could be implemented:

The object and the data class represent the two possibilities that a list can be. The MyNil object represents an empty list and MyCons represents a non-empty list. (Cons is short for "construct".) If there is only one item in the list, the tail is MyNil.

This is what it looks like to create a list:

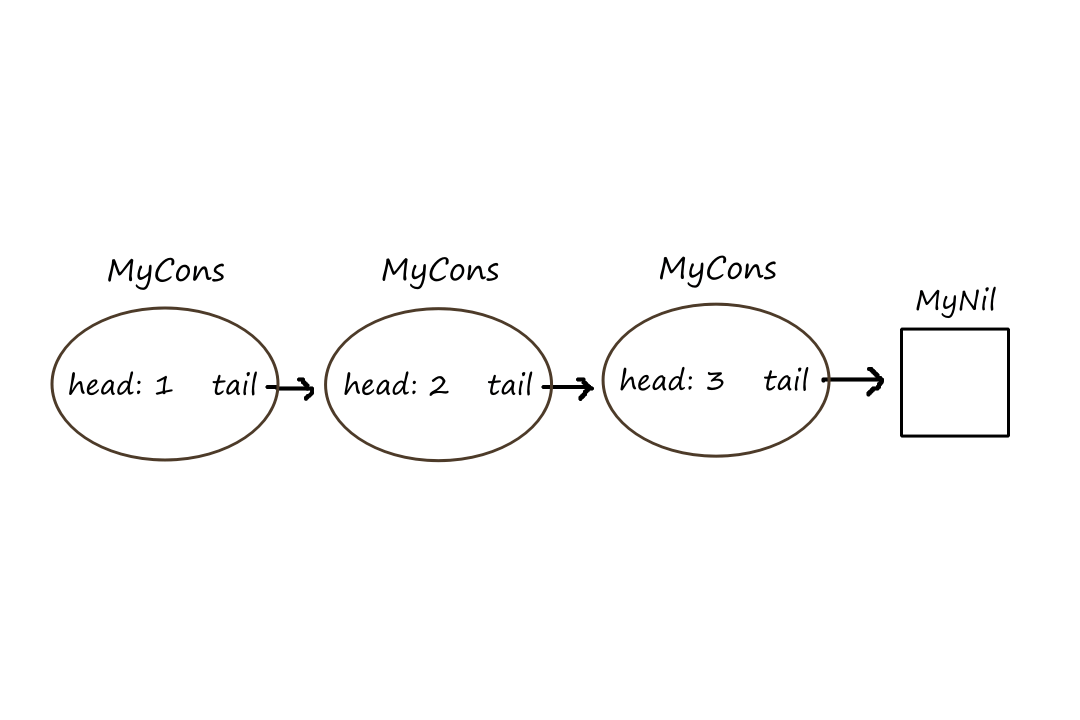
It is a little bit complicated to create lists this way. We can make it easier by creating a function similar to Kotlin's listOf() function.

In addition (😏), we can define functions to compute the sum (😏) and product of all the elements in our list.

Data Sharing

Now for the million-dollar question: since MyList is a functional data structure, how do we add and remove elements from MyList?

Let's say we wanted to add an element to the front of a list. In this case, we return a new list with the element we want to add as the head and the existing list as the tail:

If we want to remove an element from the front of a list, we return the list's tail:

A (perhaps) subtle thing to note here is that we're not actually creating new lists and copying over the values from the existing list to the new list; We're reusing the reference to the existing list. This is called data sharing.

Error Handling

As mentioned in the "Side Effects" section, throwing an exception is not functional programming. This is because throwing an exception interrupts the normal flow of the program, so now whatever was in charge of running the application has to change what it was expecting (normal execution) and deal with it.

Exceptions Break Referential Transparency

Recall that referential transparency is the ability to replace an expression with a constant value if the expression will always evaluate to the same value.

Throwing exceptions break referential transparency. Consider this function:

If we call this function, we will get an error message at runtime: 'Exception in thread "main" java.lang.Exception: boom'.

If this function was referentially transparent, we should be able to replace y with its value without changing the result of the function call.

However, if we call this function, the exception will be caught and `43` will be printed out.

Dealing with Exceptions

Exceptions can't be avoided, but if they can't be thrown, then how do we deal with them?

Consider this function where we might want to handle the exception of dividing by `0`:

Approach 1: Sentinel Value

Instead of throwing the exception, we can return some dummy value, like null, `-1`, or Double.NaN.

Drawbacks of Using a Sentinel Value

The caller may forget to check if the sentinel value was returned and treat it as a normal value, resulting in logic errors.

If using polymorphic code, there may not be a sentinel value of the correct type for certain output types. For example, if the function is taking in a list of As, we can't invent a value of type A.

Approach 2: Supplied Default Value

Instead of us deciding what to return, we can pass the decision over to the caller.

Approach 3: New Classes (Preferred Approach)

Instead of returning predefined values, we can create our own values to represent errors (and successes).

Option

When a function is defined for an input, a Some object is returned. When a function is undefined for an input, the None object is returned.

Applying this to our mean function:

Drawbacks of Using Option

An Option doesn't tell us anything about what went wrong or why the error occurred.

Either

For successful function calls, we return a Right object (because it's right!). For errors, we return a Left object (because it's not right!).

The Either data type has two values. The left (type E) is the value representing an error and the right (type A) is the value representing the result of a function.

Applying this to our mean function:

Strictness and Laziness

Strict evaluation means that expressions are evaluated and bound to variables when they are defined. Lazy evaluation means that expressions are evaluated only when they are used. Note that this means a variable can be assigned an expression, but that expression may not necessarily be evaluated. I promise this makes more sense with examples.

Stepping away from Kotlin for just a second, consider this line of code in some language:

Under strict evaluation, this results in an error because the 1/0 part will be evaluated right away. But under lazy evaluation, this line of code will print `4` since the values of the elements in the list aren't needed for the length() function.

In fact, we're more familiar with lazy evaluation than we might think. The short-circuiting logic in the && and || operators are examples of lazy evaluation.

Lazy Behavior With Functions

Functions can be non-strict where they accept arguments without evaluating them. This is done by having the functions take functions (rather than values) as arguments and calling the functions only when needed.

This is an example of a non-strict function:

To verify that this is actually a non-strict function, we can take advantage of print statements:

What is printed is a and b (each only once). If this wasn't a non-strict function, then each of a and b would've been printed twice since the arguments would have been evaluated right away.

Lazy Behavior With Ranges

Consider this code:

The output of the first println() is `1...1000000000000`. The output of the second println() is `[1, 2, 3, 4, 5]`. But the third println() fails because there should not be enough memory to store `5,000,000` numbers.

Notice that there was not enough memory for `5,000,000` numbers, but running val r: LongRange = 1..1000000000000 was fine. This shows that the range isn't evaluated right away; only when it's used.

Lazy Initialization in Kotlin

Lazy initialization is the tactic of delaying the creation of an object, calculation of a value, or execution of an expensive process until the first time it is needed. Kotlin has a built-in function called lazy to accomplish this.

First, we'll look at greedy initialization.

Here, we're passing in a function that prints "hi" and evaluates to `42`. maybeTwice() takes in that function and calls it twice, which means that "hi" will be printed twice.

Calling the function twice should result in the same thing. So why should we spend time running the function a second time if we already know its value? This is where lazy comes in.

The first time j is referenced, it calls the function i(). The value of j is then cached so that when j is called the second time, it refers to the cached value instead of running i() again. And we can verify this with the same main() code above to see that "hi" is printed only once.

Lazy Lists

From here, we'll continue by looking at a problem and building up the pieces towards a solution.

Consider this line of code:

We start with a list of `[1,2,3,4]`, add `10` to each number, get only the even numbers, and multiply those even numbers by `3`. Under the hood, multiple lists are being created at each step.

1. map{ it + 10 } creates an intermediate list (`[11,12,13,14]`)
2. filter{ it % 2 == 0 } creates an intermediate list (`[12,14]`)
3. map{ it * 3 } creates the final list (`[36,42]`)

The problem with this is that it's inefficient to create intermediate lists that are used only as inputs to the next step and never used again. We can run into memory issues if the intermediate lists are very large.

We can avoid this problem of creating temporary data structures by using laziness to combine sequences of transformations into a single pass.

Stream

We'll create a Stream to store the elements in a way that is convenient to perform transformations on them.

Since the head is a function, we need a way to evaluate the function when we need its value. We'll do this with an extension function called headOption():

And we'll need a way to create a Stream with elements:

Here's an example of creating a Stream:

(Note: this won't work in the Kotlin playground.) And this is the output:

Now this is where everything starts to come together. Recall that the problem we were trying to solve was to not create intermediate lists for code like this:

Referring back to the card analogy, what we would like to do is to look at the list one element at a time, perform all those transformations on that element, and add the result to the final list. We can do this by building off of the idea behind Kotlin's fold() function.

We'll need a custom fold-like function that works with our Stream.

z() acts as the accumulator and f() is the function that is applied to each element in the Stream.

Now, instead of using Kotlin's filter() and map(), we can use foldRight() to write our own versions of filter and map that work with our Stream.

With these versions of filter and map, we have now solved the problem of creating temporary lists! Let's look at the steps involved for

1. Stream.of(1, 2, 3, 4).map{ it + 10 }.filter{ it % 2 == 0 }.map{ it * 3 }
2. Cons({ 11 }, { Stream.of(2, 3, 4).map{ it + 10 } }).filter{ it % 2 == 0 }.map{ it * 3 }
3. Stream.of(2, 3, 4).map{ it + 10 }.filter{ it % 2 == 0 }.map{ it * 3 }
4. Cons({ 12 }, { Stream.of(3, 4).map{ it + 10 } }).filter{ it % 2 == 0 }.map{ it * 3 }
5. Cons({ 12 }, { Stream.of(3, 4).map{ it + 10 }.filter{ it % 2 == 0} }).map{ it * 3 }
6. Cons({ 36 }, { Stream.of(3, 4).map{ it + 10 }.filter{ it % 2 == 0}.map{ it * 3 } })

This is what (I believe) it actually looks like at the end. We only applied all the transformations on the first element, and if it didn't make it through all of them, then we moved on to the next element until that element completed all the transformations. The transformations aren't applied to the rest of the elements until they need to be (e.g., when examineStream() is calling s.tail()).

Corecursion

Corecursion is kinda the opposite of recursion in a way. It uses recursion to generate data instead of, well, whatever you decide to use recursion for. It may seem weird, but there's no base case or termination condition in corecursion. This allows us to create infinite data structures that aren't actually infinite.

We can have something a little more useful than an infinite Stream of just `1`s.

Memoization

Let's look at the classic example of calculating the Fibonacci numbers.

If we were to do this in code, it would look like this:

As can be inferrred from the name, this way of calculating the Fibonacci numbers is very inefficient. Consider the example of calculating the `5^(th)` Fibonacci number.

Look at how many of the calculations are repeated. Not only is it wasteful, it's actually time-consuming. Instead of recalculating the same values for which we already the answer, we can store them so that we can reuse them when we need to — this is memoization! We actually saw this in action in the "Lazy Initialization in Kotlin" section with Kotlin's lazy function.

We'll use our Stream to generate an infinite sequence of Fibonacci numbers.

To utilize laziness, we'll define a smart constructor, which is a function for constructing a data type that has a slightly different signature than the real constructor.

This ensures that the thunk will only be called once when forced for the first time. Subsequent forces will return the cached values from using lazy.

So this is how we would generate Fibonacci numbers without recalculating old Fibonacci numbers:

So here's the improved version of calculating Fibonacci numbers:

Functional State

Program state refers to the values of the variables, data structures, and other information (e.g., the address of next line to execute, the status of I/O operations) that describe the current state of the program at a specific point in time. In functional programming, changes to program state are undesirable.

So to manipulate program state in a functional way, we view the program state as a transition or action that can be passed around. This keeps the state contained and localized.

Generating Random Numbers

We'll look at how to pass around state by looking at random number generation.

If we wanted to generate random numbers in Kotlin, we would do something like this:

As we expect, `3` numbers will be printed. Also as we expect, if we run these lines again, then `3` potentially different numbers will be generated. Since calling the same function with the same inputs produces different outputs, nextInt() is not referentially transparent. While we don't know exactly how nextInt() is implemented, we can see that there is some sort of state mutation happening.

Let's see how we can generate random numbers in a functional manner.

Forget about the details of the algorithm. The important thing to note is that our new nextInt() function is returning two things here: a random number and a random number generator.

If we run these lines multiple times, we'll get the same `3` numbers every time.

So what exactly did we do to make this possible? We made the state change explicity known by asking for a seed and returning the new state instead of implicitly mutating the original state.

Stateful APIs

Stateful APIs are interfaces in which the next state depends on the previous state. (Here, stateful means that we're creating a new state and using that to do stuff.) Our RNG is an example of a stateful API, and we'll look at how to extend it.

Let's say we wanted to write a function that generates a pair of random numbers using nextInt().

By returning rng3, we're allowing the caller to generate more random numbers if they need to.

There's a common pattern (which can be seen in the exercises above) where functions that need to return a value and a state return them as a Pair. These functions have a type of the form (RNG) -> Pair<A, RNG> for some type A. Functions of this type are called "state actions" or "state transitions" because they transform states from one call to the next.

Combinators

State actions can be combined using combinators, which are higher-order functions that combine or transform functions in some way to produce new functions.

map is a combinator that takes an RNG function (passed in as s) and applies f to the random number that is generated by s. Here's an example using it:

So we're taking the random integer generated by nonNegativeInt and dividing it by (Int.MAX_VALUE.toDouble() + 1).

Now here's something that's a little more complicated. We can take two state actions and apply a binary function to them:

So we're taking the random numbers generated by intR (passed as ra)and doubleR (passed as rb) and creating a Pair with them (using the lambda { a, b -> a to b }).

Monoids

No, it's not some infectious disease. In math (specifically, abstract algebra), a monoid is a set that has an associative binary operation and an identity element.

In programming, a monoid is a type with an associative binary operation and an identity element. We can create a monoid with the string concatenation operator. String concatenation is associative and the identity element is the empty string.

We can express a monoid in Kotlin as an interface:

And create a monoid by implementing it:

Here's another way with a monoid instance:

So what are monoids used for anyway? From the lecture slides:

• A monoid can be used as an abstraction
• We can write generic code, assuming only the capabilities provided by the fact that the abstraction is a monoid

Whatever that means.

It turns out that monoids are helpful for things like combining data structures and aggregating results. Monoids make it possible to do those things in a parallel manner, which we're about to see.

Lists and Monoids

foldLeft() and foldRight() are custom implementations of fold() that we can define if we want to iterate over the collection in a certain order. foldLeft() starts at the beginning and iterates to the end (left to right), while foldRight() starts at the end and iterates backwards to the beginning (right to left).

If we call foldLeft() and foldRight() with a monoid, then we should get the same result for both functions (since the operation is associative).

The problem with foldLeft() and foldRight() is that they aren't efficient when the lists are very large (they iterate one element at a time). We can solve this by taking advantage of the fact that the operator in a monoid is associative, meaning that we can start from anywhere, combine the results in any way, and still get the same result as if we iterated one element at a time.