Combinatorics
(or as I like to call it, combinatrix)
Shortcut to this page: ntrllog.netlify.app/comb
Notes provided by Professor Steven Sam (UCSD)
Formulas
Number of subsets: `sum_(k=0)^n ((n),(k)) = 2^n`
Pascal's Identity: `((n),(k)) + ((n),(k-1)) = ((n+1),(k))`
Number of `k`-element multisets: `((n+k-1),(k))`
Number of weak compositions into `k` parts: `((n+k-1),(n))`
Number of compositions into `k` parts: `((n-1),(n-k)) = ((n-1),(k-1))`
Number of compositions into all possible parts: `2^(n-1)`
Number of set partitions into `k` blocks: `S(n,k) = S(n-1,k-1) + k*S(n-1,k)`
Bell numbers: `B(n+1) = sum_(i=0)^n ((n),(i))B(i)` and `B(0)=1`
Binomial Theorem: `(x+y)^n = sum_(i=0)^n ((n),(i)) x^iy^(n-i)`
Multinomial Theorem: `(x_1+x_2+...+x_k)^n = sum_(a_1+a_2+...+a_k=n) ((n),((a_1, a_2, ..., a_k))) x_1^(a_1)x_2^(a_2)...x_k^(a_k)`
`sum_(n ge 0) x^n = 1/(1-x)`
Binomial Theorem (General): `(1+x)^m = sum_(n ge 0)((m),(n))x^n`
`((-d),(n)) = (-1)^n((d+n-1),(n)) = (-1)^n((d+n-1),(d-1))`
`(1+x)^(-d) = sum_(n ge 0) (-1)^n((d+n-1),(n))x^n = sum_(n ge 0) (-1)^n((d+n-1),(d-1))x^n`
Product of ogf: `A(x)B(x) = sum_(n ge 0)(sum_(i=0)^na_ib_(n-i))x^n`
Composition of ogf: `B(A(x)) = sum_(n ge 0) b_nA(x)^n`
Catalan numbers: `C_n = 1/(n+1) ((2n),(n))`
Catalan numbers (recurrence): `C_n = sum_(i = 0)^(n-1)C_iC_(n-1-i)` and `C_0 = 1`
`sum_(n ge 0) x^n/(n!) = e^x`
Product of egf: `A(x)B(x) = sum_(n ge 0)(sum_(i=0)^n((n),(i))a_ib_(n-i))x^n/(n!)`
Lagrange Inversion: If `A(x) = xG(A(x))`, then `[x^n]A(x) = 1/n[x^(n-1)](G(x)^n)`
- `G(x)` must have a nonzero constant term
Inclusion-Exclusion: `|A_1 uu A_2 uu ... uu A_n| = sum_(j=1)^n(-1)^(j-1)sum_(1 le i_1 lt i_2 ... lt i_j le n)|A_(i_1) nn A_(i_2) ... nn A_(i_j)|`
Number of derangements: `sum_(i=0)^n(-1)^i(n!)/(i!)`
Number of necklaces: `sum_(d|n)(omega(d))/d`
- `omega(d)` is the number of words with period `d`
`omega(d) = sum_(e|d)mu(d/e)k^e`
Induction
Theorem: There are `2^n` subsets of a set of size `n`
Let `P(n)` be the statement that there are `2^n` subsets of a set of size `n`
For a set with `0` elements, the only subset is `O/`, which is consistent with `2^0 = 1` so `P(0)` is true
Suppose `P(n)` is true. Want to show `P(n+1)` is true, i.e., there are `2^(n+1)` subsets of a set of size `n+1`
Let `S` be a set of size `n+1`
Fix any `x in S` and consider `S' = S\\{x}`
Since `S'` has `n` elements, there are `2^n` subsets
Every subset of `S` either contains `x` or it doesn't contain `x`
The subsets that don't contain `x` are in `S'`, which has `2^n` subsets
So there are `2^n` subsets that don't contain `x`
The subsets that do contain `x` can be obtained by adding `x` to each of the `2^n` subsets that don't contain `x`
So there are `2^n` subsets that do contain `x`
The total number of subsets of `S` is the number of subsets containing `x` plus the number of the subsets not containing `x`
So the total number of subsets of `S` is `2^n + 2^n = 2*2^(n) = 2^(n+1)`
So `P(n+1)` is true
`sum_(i=0)^n i = (n*(n+1))/2`
Let `P(n)` be the statement `sum_(i=0)^n i = (n*(n+1))/2`
For `n=0`, `sum_(i=0)^0 i = 0` and `(0*(0+1))/2 = 0` so `P(0)` is true
Suppose `P(n)` is true. Want to show `P(n+1)` is true, i.e., `sum_(i=0)^(n+1) i = ((n+1)(n+2))/2`
`sum_(i=0)^(n+1) i = sum_(i=0)^n i + (n+1)`
`= (n*(n+1))/2 + (n+1)`
`= (n^2 + n)/2 + (2(n+1))/2`
`= (n^2 + n)/2 + (2n + 2)/2`
`= (n^2 + 3n + 2)/2`
`= ((n+1)(n+2))/2`
So `P(n+1)` is true
`4n lt 2^n` for `n ge 5`
Let `P(n)` be the statement `4n lt 2^n` for `n ge 5`
For `n=0`, `4*0 = 0 lt 2^0 = 1` so `P(0)` is true
Suppose `P(n)` is true. Want to show `P(n+1)` is true, i.e., `4n+4 lt 2^(n+1)`
`2^(n+1) = 2*2^n`
`= 2^n + 2^n`
`gt 4n + 4n`
`gt 4n + 4` (since `n ge 5`)
So `P(n+1)` is true
Every polynomial in `x` is a linear combination of `1, x-1, (x-1)^2, (x-1)^3, ...`
Let `P(n)` be the statement that every polynomial of degree `n` in `x` is a linear combination of the powers of `x-1`
For `n=0`, the polynomial of degree `0` is a constant `c`, which is a linear combination of `1` (`c = c*1`) so `P(0)` is true
Suppose `P(0), P(1), P(2), ... P(n)` is true. Want to show `P(n+1)` is true, i.e., every polynomial of degree `n+1` in `x` is a linear combination of the powers of `x-1`
Let `f(x)` be a polynomial of degree `n+1`
Let `alpha` be the leading coefficient of `f`
Consider `g(x) = f(x) - alpha*(x-1)^(n+1)`
`g(x)` is a polynomial of degree `le n` so it is a linear combination of the powers of `x-1`
`f(x) = g(x) + alpha*(x-1)^(n+1)`
`alpha*(x-1)^(n+1)` is also a linear combination of the powers of `x-1`
So `f(x)` is a linear combination of the powers of `x-1`
So `P(n+1)` is true
Every positive integer can be written as `2^rm` where `r ge 0` and `m` is an odd integer
Let `P(n)` be the statement that `n` can be written as `2^rm` where `r ge 0` and `m` is odd
For `n=1`, `1 = 2^0*1 = 1` so `P(1)` is true
Suppose `P(1), ..., P(n)` is true. Want to show `P(n+1)` is true, i.e., `n+1` can be written as `2^rm` where `r ge 0` and `m` is odd
Suppose `n+1` is odd. Then pick `r=0` and pick `m = n+1` so `P(n+1)` is true
Suppose `n+1` is even
Then it can be written as `n+1 = 2k` for some integer `1 le k le n`
Since `k` is a positive integer, it can be written as `2^rm` where `r ge 0` and `m` is odd
`n+1 = 2k`
`= 2*2^rm`
`= 2^(r+1)m`
`m` is odd and `r ge 0 implies r+1 ge 0` so `n+1` can be written as a power of `2` multiplied by an odd number
So `P(n+1)` is true
Every integer `n ge 2` can be written as a product of prime numbers
Let `P(n)` be the statement that `n` can be written as a product of prime numbers
For `n=2`, `2` is a product of `2`, which is a prime number so `P(2)` is true
Suppose `P(2), ..., P(n)` is true. Want to show `P(n+1)` is true, i.e., `n+1` can be written as a product of prime numbers
Suppose `n+1` is prime. Then it is a product of itself so `P(n+1)` is true
Suppose `n+1` is not prime
Then `n+1` can be written as `n+1 = a*b` for integers `a,b` where `2 le a,b le n`
Since `2 le a,b le n`, `a` and `b` can be written as products of prime numbers
So `n+1` is a product of prime numbers
So `P(n+1)` is true
Let `f` be a function so that `f(0)=1`, `f(1)=2`, and `f(n+1)=f(n-1)+2f(n)` for `n ge 1`. Show that `f(n) le 3^n` for `n ge 0`
Let `P(n)` be the statement that `f(n) le 3^n` for `n ge 0`
For `n=0`, `f(0) = 1 le 3^0 = 1`
For `n=1`, `f(1) = 2 le 3^1 = 3`
So `P(0)` and `P(1)` are true
Suppose `P(n)` is true. Want to show that `P(n+1)` is true, i.e., `f(n+1) le 3^(n+1)`
`f(n+1) = f(n-1)+2f(n)`
`le 3^(n-1) + 2*3^n`
`= 3^(n-1) + 3^n + 3^n`
`le 3^n + 3^n + 3^n`
`= 3*3^n`
`= 3^(n+1)`
So `P(n+1)` is true
Permutations
Given a set `S` of objects, a permutation of `S` is a way to put all elements of `S` in order
Example: For `S = {1,2,3}`, all the permutations are:
`1,2,3`
`1,3,2`
`2,1,3`
`2,3,1`
`3,1,2`
`3,2,1`
Theorem: If `S` has `n gt 0` elements, then there are `n!` permutations of the elements in `S`
Let `P(n)` be the statement that if `S` has `n gt 0` elements, then there are `n!` permutations of the elements of `S`
For a set of size `1`, there's only `1` way to order all the elements. `1 = 1!` so `P(1)` is true
Suppose `P(n)` is true. Want to show `P(n+1)` is true, i.e., if `S` has `n+1` elements, then there are `(n+1)!` permutations of the elements in `S`
Let `S` be a set of size `n+1`
We could pick any random element of `S` and put that in the first spot
There are `n+1` choices for the random element in the first spot
Now, `S` has `n` elements
So there are `n!` ways to order the remaining elements in `S`
So the total number of ways to order the elements is `(n+1)*n! = (n+1)!`
So `P(n+1)` is true
Intuitively, there are `n` choices for the first digit, `n-1` choices for the second digit, `n-2` choices for the third digit, ..., all the way down to `1` choice for the last digit
So there are `n*(n-1)*(n-2)*...*1 = n!` ways to order the elements
Combinations
Let's suppose we're arranging flowers. We have `2` red flowers and `1` yellow flower. How many ways can we arrange them? Previously, we saw that if we have `n` elements, there are `n!` ways to arrange them. Here, we have `3` elements, so there are `3! = 6` ways to arrange them. All the possible orderings are:
`R RY`
`R RY`
`YR R`
`YR R`
`RYR`
`RYR`
But some of the orderings are repeated. This is because the `2` red flowers are technically different flowers, but the order in which they appear doesn't matter; the result is the same. So we have to divide out the commonalities. In this case, since there are `2` red flowers and, therefore, `2!` ways to order them, we divide the total number of ways to arrange all the elements by `2!`.
`(3!)/(2!) = 3`
`R RY`
`YR R`
`RYR`
If we have `10` red flowers and `5` yellow flowers, then the total number of ways to arrange them is
`(15!)/(10!5!)`
If we have `r` red flowers, `y` yellow flowers, and `b` blue flowers, then the total number of ways to arrange them is
`((r+y+b)!)/(r!y!b!)`
Theorem: Say we have `n` objects which have one of `k` different types. Objects of the same type are considered identical. Label the types with numbers `1,2,...,k` and let `a_i` be the number of objects of type `i`. Then the number of ways to arrange the `n` objects is `(n!)/(a_1!a_2!...a_k!)`
The multinomial coefficient is
`((n),((a_1,a_2,...,a_k))) = (n!)/(a_1!a_2!...a_k!)`
The binomial coefficient is the multinomial coefficient for `k=2`, which is
`((n),((a_1,a_2)))`
It's often denoted by
`((n),(a_1))`
instead because we know `a_2 = n - a_1`
Words
Sometimes, it's easier to count things by using some sort of encoding.
A word is a finite ordered sequence whose entries are drawn from some set `A`, called the alphabet
The length of a word is the number of entries it has
Entries may be repeated
An empty sequence `O/` is a word of length `0`
Example: Consider the alphabet `A = {a,b}`
The words of length `le 2` are:
`O/`
`a`
`b`
`aa`
`ab`
`ba`
`bb`
Theorem: If `|A| = n`, then the number of words of length `k` is `n^k`
There are `k` spots, and each spot has `n` choices of entries
So there are `ubrace(n*n*...*n)_k = n^k` words of length `k`
`[n] = {1,2,...,n}`
The number of subsets of `[n]` is `2^n`
Let `S sube [n]`
Define a word `w_s` of length `n` in the alphabet `{0,1}` as follows:
Let `i in [n]`
If `i in S`, then the `i^(th)` entry of `w_s = 1`
If `i notin S`, then the `i^(th)` entry of `w_s = 0`
If `n = 5` and `S = {1,3,4}`, then the word associated with `S` is `10110`
Define a function `f:{`subset `S` of `[n]} rarr {`word of length `n` in alphabet `{0,1}}`
We can define another function `g:{`words of length `n` in `{0,1}} rarr {`subset of `[n]}`
The process for converting a subset to a word is reversible, gives a unique result, and always gives a result with valid input
So `g` is the inverse of `f`, which means `f` is bijective
So `|{`subsets of `[n]}| = |{`words of length `n` in `{0,1}}| = 2^n`
The general idea is that any element is either in `S` or not in `S`
How many pairs of subsets `S,T sube [n]` satisfy `S sube T`?
Any element in `[n]` is
- in `S` and in `T`
- not in `S` but in `T`
- not in `S` and not in `T`
There are `3` choices for each of the `n` elements, so there are `3^n` total possibilities
In the context of words, the function would be
`f:{`pairs of subsets `S,T sube [n]` s.t. `S sube T} rarr {`words of length `n` in `{`in `S`, not in `S` but in `T`, not in `S` and not in `T}}`
For `n ge k` where `n` is a nonnegative integer, the falling factorial is
`(n)_k = n*(n-1)*(n-2)*...*(n-k+1)`
`(6)_3 = 6*5*4`
`(6)_6 = 6*5*4*3*2*1`
There are `k` numbers being multiplied
This can be seen by:
`(n)_k = n*(n-1)*(n-2)*...*(n-k+1)`
`= (n-0)*(n-1)*(n-2)*...*(n-(k-1))`
There are `k` numbers from `0` to `k-1`
Theorem: If `|A| = n ge k`, then there are `(n)_k` words of length `k` in `A` that do not have repeating entries
Let `sigma = a_1a_2...a_ka_(k+1)...a_n` be a permutation of `A`
The first `k` entries make up a word with no repeating entries
Since there are `n!` permutations, we have `n!` words with no repeating entries
But there are repeated words since the last `(n-k)` entries can be ordered in any way
So there are
`(n!)/((n-k)!) = (n*(n-1)*...*(n-k+1)*(n-k)!)/((n-k)!)`
`= n*(n-1)*...*(n-k+1)`
`= (n)_k`
words with no repeating entries
Let `A = {1,2,3,4,5}` and `k=3`
Let `sigma = 31254`
The first `k` entries are `312`, which is a word of length `k` with no repeating entries
So that is contained in `31254`
But that same word is also contained in `31245`
Intuitively, there are `n` choices for the first digit, `n-1` choices for the second digit, ..., `n-k+1` choices for the `k^(th)` digit
Choice Problems
We saw earlier that the number of subsets of a set of size `n` is `2^n`. We could look at how many of those subsets are of size `k`.
Theorem: The number of `k`-element subsets of `[n]` is `((n),(k)) = (n!)/(k!(n-k)!)`
We can associate subsets of `[n]` with words of length `n` in `{0,1}`
The number of `k`-element subsets of `[n]` is the number of words of length `n` in `{0,1}` that have exactly `k` `1`'s
For such words, there are `k` ways to arrange the `1`'s and `n-k` ways to arrange the `0`'s
Which gives us `(n!)/(k!(n-k)!) = ((n),(k))`
Corollary: `sum_(k=0)^n ((n),(k)) = 2^n`
`sum_(k=0)^n ((n),(k))` is the number of ways to choose subsets of size `0`, `1`, `2`, ..., `n`
Well, that should make up all the possible subsets
Before, we showed that the total number of subsets is `2^n`
Pascal's Identity: `((n),(k-1)) + ((n),(k)) = ((n+1),(k))` for any `k ge 0`
`((n+1),(k))` is the number of `k`-element subsets of `[n+1]`
We could split those subsets up into two categories: subsets of size `k` that contain `n+1` and subsets of size `k` that don't contain `n+1`

The subsets of size `k` that don't contain `n+1` are actually the subsets of size `k` of `[n]`, so that gives us `((n),(k))`
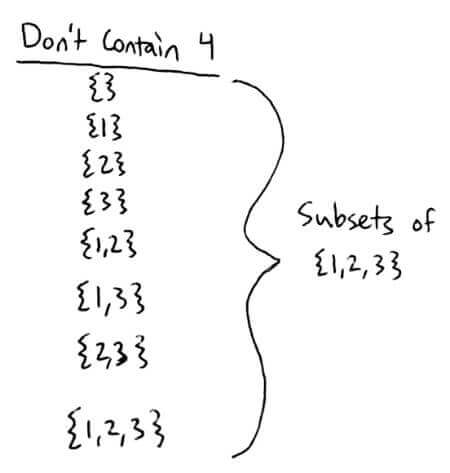
If we look at the subsets of size `k` that do contain `n+1` and remove `n+1` from each subset, we end up with the number of subsets of size `k-1` of `[n]`, which gives us `((n),(k-1))`
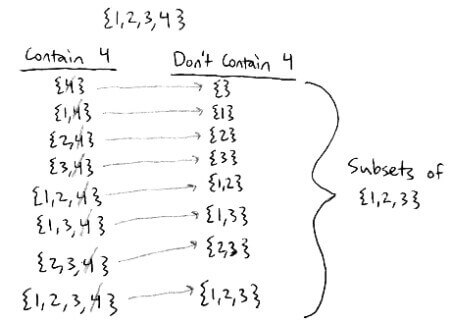
These two sets don't overlap so there are `((n),(k))+((n),(k-1))` subsets of size `k` of `[n+1]`
Counting Poker Hands
Four of a Kind: `4` of the `5` cards have the same value
How many four of a kinds are there?
There are `13` choices for the value that is the same
There are `48` choices for the fifth card
Total number of ways to get a four of a kind: `13*48`
Alternatively,
There are `13` choices for the value that is the same
There are `12` choices for the value that is different
There are `4` choices for the suit of the different value
Total number of ways to get a four of a kind: `13*12*4`
Full House: `3` cards have the same value and `2` cards have the same value
How many full houses are there?
There are `13` choices for the value of the triple
There are `12` choices for the value of the pair
There are `((4),(3))` choices for the suits of the triple
There are `((4),(2))` choices for the suits of the pair
Total number of ways to get a full house: `13*12*((4),(3))*((4),(2))`
Two Pair: `2` cards have the same value, `2` cards have the same value, `1` card has a different value
How many two pairs are there?
There are `((13),(2))` choices for the value of each pair
There are `((4),(2))` choices for suits of one pair
There are `((4),(2))` choices for suits of other pair
There are `44` choices for the leftover card
Total number of ways to get a two pair: `((13),(2))*((4),(2))*((4),(2))*44`
Alternatively,
There are `((13),(2))` choices for the value of each pair
There are `11` choices for the value of the different card
There are `((4),(2))` choices for suits of one pair
There are `((4),(2))` choices for suits of other pair
There are `4` choices for the suit of the different card
Total number of ways to get a two pair: `((13),(2))*11*((4),(2))*((4),(2))*4`
Straight: `5` cards can be put in consecutive order by values
How many straights are there?
To pick values, we only need to know what the largest possible values are
The fifth card can be `5`, `6`, `7`, `8`, `9`, `10`, `J`, `Q`, `K`, or `A`
There are `10` choices for the fifth card
There are `4^5` choices for the suits of each card
Total number of ways to get a straight: `10*4^5`
Multisets
Multisets are like subsets except the elements can be repeated.
Multisets of `{1,2,3}` of size `3` are:
`{1,1,1}`
`{1,1,2}`
`{1,1,3}`
`{1,2,2}`
`{1,2,3}`
`{1,3,3}`
`{2,2,2}`
`{2,2,3}`
`{2,3,3}`
`{3,3,3}`
Are these all the possible multisets? How can we be sure?
Let's add `1` to the second element and add `2` to the third element
`{1,1,1} rarr {1,2,3}`
`{1,1,2} rarr {1,2,4}`
`{1,1,3} rarr {1,2,5}`
`{1,2,2} rarr {1,3,4}`
`{1,2,3} rarr {1,3,5}`
`{1,3,3} rarr {1,4,5}`
`{2,2,2} rarr {2,3,4}`
`{2,2,3} rarr {2,3,5}`
`{2,3,3} rarr {2,4,5}`
`{3,3,3} rarr {3,4,5}`
Notice that we end up with all the subsets of size `3` of `[5]`. This leads to a more general result
Theorem: The number of `k`-element multisets of a set of size `n` is `((n+k-1),(k))`
Note: it doesn't matter what the set is, since we can form a bijection between the set and `[n]`
Let `S` be a multiset of size `k` of `[n]`
Sort the elements of `S` so that `s_1 le s_2 le s_3 le ... le s_k`
Add `i-1` to each `s_i`
Then we get `s_1 lt s_2 + 1 lt s_3 + 2 lt ... lt s_k + (k-1)`
Well, `{s_1, s_2+1, s_3+2, ..., s_k+(k-1)}` is a subset of size `k` of `[n+k-1]color(red)(text(*))`
The number of ways to make `k`-element subsets from a set of size `[n+k-1]` is `((n+k-1),(k))`
(Reversing the process -- subtracting `i-1` from each `s_i` -- shows that there is a bijection between `{s_1, s_2, ..., s_k}` and `{s_1, s_2+1, ..., s_k+(k-1)}`)
`color(red)(text(*))` happens when `s_k = n`
Let `x`,`y`,`z` be variables. The degree of the monomial `x^ay^bz^c` is `a+b+c` where `a,b,c ge 0`
How many monomials have degree `d`?
There are `3` with degree `1`:
`x,y,z`
There are `6` with degree `2`:
`x^2,y^2,z^2,xy,xz,yz`
There are `10` with degree `3`:
`x^3,y^3,z^3,x^2y,x^2z,y^2x,y^2z,z^2x,z^2y,xyz`
`x^ay^bz^c` is like a multiset of `{x,y,z}` where `x` appears `a` times, `y` appears `b` times, and `z` appears `c` times
Since they add up to `d`, there should be `d` total elements
So the total number of monomials is the number of multisets of size `d` of `{x,y,z}`, which is
`((d+3-1),(d)) = ((d+2),(d))`
Let `x_1,x_2,...,x_n` be variables. How many monomials `x_1^(a_1)*x_2^(a_2)*...*x_n^(a_n)` are there with degree `d`?
`x_1^(a_1)*x_2^(a_2)*...*x_n^(a_n)` is like a multiset of `{x_1,x_2,...,x_n}` where each `x_i` is chosen `a_i` times
Since they add up to `d`, there should be `d` total elements
So the total number of monomials is the number of multisets of size `d` of `{x_1,x_2,...,x_n}`, which is
`((n+d-1),(d))`
Compositions
A weak composition of `n` into `k` parts is a `k`-tuple `(a_1,a_2,...,a_k)` such that each `a_i ge 0` and `a_1 + a_2 + ... + a_k = n`
A composition is the same except each `a_i gt 0`
`k` is the number of parts
Theorem: The number of weak compositions of `n` into `k` parts is `((n+k-1),(n))`
Claim: There is a bijection between weak compositions of `n` into `k` parts and `n`-element multisets of `[k]`
Given a weak composition `(a_1,...,a_k)`, we get a multiset that has the `i^(th)` element `a_i` times
Since `a_1 + ... + a_k = n`, this is an `n`-element multiset of `[k]`
Given an `n`-element multiset of `[k]`, let `a_i` be the number of times that `i` appears in the multiset
Then we end up with a weak composition `(a_1,...,a_k)` of `n`
Intuitively, a multiset is a weak composition that is written out. Since the parts of the weak composition have to add up to `n`, there are `n` elements in the multiset. So the formula for an `n`-element multiset applies here.
`((n+k-1),(n)) = ((n+k-1),(n+k-1-n)) = ((n+k-1),(k-1))`
How many ways are there to distribute `20` identical pieces of candy to `4` different children?
This can be seen as a weak composition of `20` into `4` parts
`((23),(20))`
How many ways can we distribute all the candy so that no child is candyless?
First, we can give each child `1` piece of candy
Now, we have `16` pieces of candy leftover which can be distributed in any way
So this can be seen as a weak composition of `16` into `4` parts
`((19),(16))`
Since each child has at least `1` candy, this is also a composition of `20` into `4` parts
Corollary: The number of compositions of `n` into `k` parts is `((n-1),(n-k))`
Generalizing the previous example, there is a bijection between compositions of `n` into `k` parts and weak compositions of `n-k` into `k` parts
`(((n-k)+k-1),(n-k)) = ((n-1),(n-k)) = ((n-1),(n-1-(n-k))) = ((n-1),(k-1))`
Corollary: The number of compositions of `n` into any number of parts is `2^(n-1)`
The possible number of parts for a composition of `n` ranges from `k = 1` to `k = n`
So the total number of compositions possible is
`sum_(k=1)^n((n-1),(k-1))`
`= sum_(k=0)^(n-1)((n-1),(k))`
Well, that is the formula for the number of subsets of `[n-1]`, which is `2^(n-1)`
A composition can be represented as `(1square1square...square1square1)` where we either put a `+` (plus sign) or a `,` (comma) in the boxes.
There are `n` `1's`, so there are `n-1` boxes
There are `2` choices for each box
So there are `2^(n-1)` total compositions
Set Partitions
Let `X` be a set. A partition of `X` is an unordered collection of nonempty subsets `X_1,...,X_k` such that every element of `X` belongs to exactly one subset
An ordered partition of `X` is the same except each subset has an order
Each subset is a block of the partition
There are `5` partitions of `X = {1,2,3}`:
`k = 1:`
`{{1,2,3}}`
`k = 2:`
`{{1},{2,3}}`
`{{2},{1,3}}`
`{{3},{1,2}}`
`k = 3:`
`{{1},{2},{3}}`
For an unordered collection of subsets, `{{3},{1,2}}` and `{{1,2},{3}}` are the same (the order of the blocks doesn't matter)
How many ways are there to distribute `20` different pieces of candy to `4` identical children so that no child is candyless?
This can be seen as a partition of `[20]` into `4` blocks
Unfortunately, there's not really a nice formula for the number of set partitions of `[n]`. But we can still count them though.
Let `S(n,k)` be the number of partitions of a set of size `n` into `k` blocks
These are called Stirling numbers of the second kind
`S(0,0) = 1` and `S(n,k) = 0` if `k gt n`
For some values of `k`, there actually are nice formulas.
`S(n,1)`
This is `n` pieces into `1` block. The only way to do this is to put all the pieces into the block
`S(n,1) = 1`
`S(n,n)`
This is `n` pieces into `n` blocks. The only way to do this is to put each piece in each block
`S(n,n)=1`
`S(n,2)`
This is `n` pieces into `2` blocks
We can't put `O/` or the whole set in the blocks, so there are `2^n-2` complementary subsets
The order of the blocks don't matter, so there are `(2^n-2)/(2!) = 2^(n-1)-1` ways to do this
`S(n,2) = 2^(n-1)-1`
`S(n,n-1)`
This is `n` pieces into `n-1` blocks
One block must have `2` pieces, so we choose `2` elements to be in the same block
`S(n,n-1) = ((n),(2))`
For other values of `k`, there is a recurrence relation that allows us to calculate `S(n,k)`.
Theorem: If `k le n`, then `S(n,k) = S(n-1,k-1) + k*S(n-1,k)`
Consider two kinds of partitions of `[n]`
The first kind is partitions where `n` is in its own block
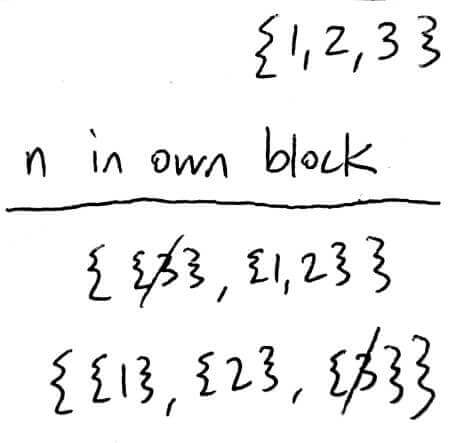
Removing that block, we end up with a partition of `n-1` into `k-1` blocks, which is `S(n-1,k-1)`
The second kind of partition is the partitions where `n` is not in its own block

Removing `n` from each partition, we end up with a partition of `n-1` into `k` blocks
But by doing so, we can't reconstruct the original situation because we don't know which block it came from
There are `k` blocks we could put `n` in `implies k` different ways to reconstruct the original situation
So the number of partitions is `k*S(n-1,k)`
Adding up both types of partitions gives us all the partitions of `[n]`
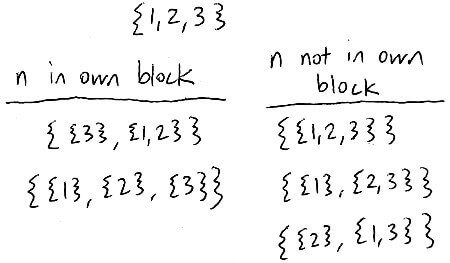
We can use this recurrence to verify that `S(n,2) = 2^(n-1)-1`
`S(n,2) = S(n-1,1) + 2*S(n-1,2)`
`= 1 + 2*S(n-1,2)`
`= 1 + 2*(2^(n-2)-1)`
`= 1 + 2^(n-1)-2`
`= 2^(n-1)-1`
The Stirling numbers counted the number of set partitions into blocks of specific sizes. To get the total number of set partitions of all sizes, we add them all up.
The Bell numbers are the number of partitions of `[n]` into any number of blocks
`B(n) = sum_(k=0)^nS(n,k)`
`B(0) = 1`
Theorem: `B(n+1) = sum_(i=0)^n ((n),(i)) B(i)`
Separate all the partitions of `[n+1]` based on the number of elements in the block that contains `n+1`
Consider those partitions where the block containing `n+1` is of size `j`
For the block containing `n+1`, there are `n` numbers to choose from and `j-1` spots, so there are `((n),(j-1))` ways to generate such a block
Now, there are `n+1-j` elements remaining
For the other blocks not containing `n+1`, they can be generated by looking at the number of partitions of `[n+j-1]`, i.e., `B(n+j-1)`
So the number of partitions where the block containing `n+1` is of size `j` is `((n),(j-1)) B(n+1-j)`
The possible sizes of blocks containing `n+1` range from `1` to `n+1`
`sum_(j=1)^(n+1) ((n),(j-1)) B(n+1-j)`
set `i = j-1`
`sum_(i=0)^n ((n),(i)) B(n-i)`
set `k = n-i`
`sum_(k=0)^n ((n),(n-k)) B(k)`
`sum_(k=0)^n ((n),(k)) B(k)`
Integer Partitions
A partition of `n` is a sequence of nonnegative integers `lambda_1 ge lambda_2 ge ... ge lambda_k ge 0` such that `lambda_1 + lambda_2 + ... + lambda_k = n`
`lambda = (lambda_1, lambda_2, ..., lambda_k)` is a partition
`|lambda| = lambda_1 + lambda_2 + ... + lambda_k`
`l(lambda)` is the length of the partition
There are no nice formulas for the number of partitions, but we have a notation for it.
`p(n) = ` number of partitions of `n`
`p_k(n) = ` number of partitions of `n` such that `l(lambda) = k` (has `k` parts)
`p(5) = 7`
`(5)`
`(4,1)`
`(3,2)`
`(3,1,1)`
`(2,2,1)`
`(2,1,1,1)`
`(1,1,1,1,1)`
Partitions can be represented using Young diagrams. The `i^(th)` row has `lambda_i` boxes.
`lambda = (4,2,1)`

The transpose (or conjugate) of a partition `lambda` is the partition `lambda^T` whose Young diagram is `Y(lambda)` flipped across the main diagonal
`(lambda^T)^T = lambda`
`lambda_i^T = {j|lambda_j ge i}`
`lambda^T = (3,2,1,1)`

`lambda` is self-conjugate if `lambda = lambda^T`
Some self-conjugate partitions are `(4,3,2,1)`, `(5,1,1,1,1)`, `(4,2,1,1)`
Theorem: The number of partitions `lambda` of `n` with `l(lambda) le k` equals the number of partitions `mu` of `n` with `mu_i le k`
Example: `n=5, k=2`
`(5)`
`(4,1)`
`(3,2)`
`(1,1,1,1,1)`
`(2,1,1,1)`
`(2,2,1)`
Notice that taking the transpose of `lambda` gives us `mu`
Claim: There is a bijection between `A = {`partitions `lambda` of `n` with `l(lambda) le k}` and `B = {`partitions `mu` of `n` such that `mu_i le k}`
Let `f:A rarr B` be a function defined to be `f(lambda) = lambda^T`
Since `(lambda^T)^T = lambda`, `f circ f` is the identity function, which means it is its own inverse
So `f` is bijective `implies |A| = |B|`
Theorem: The number of self-conjugate partitions `lambda` of `n` equals the number of partitions `mu` of `n` with only odd and distinct parts
Start with a Young diagram of `lambda`
Take the boxes of the first row and column and put them all in a row
Make that row the first row of `mu`
Repeat this for all the rows/columns of the `lambda`
(Informally, peel off the outer layer of `lambda` and straighten it out to become a row in `mu`)
This process is reversible, so there is a bijection
(Informally, fold the row of `mu` in half and make it the outer layer of `lambda`)
Since `lambda` is self-conjugate, there are an odd number of parts in the `i^(th)` row and column
Now we show why they are distinct
We can come up with a formula for the length of the `i^(th)` row
The `i^(th)` row of `mu` is the `i^(th)` row of `lambda` minus the boxes to the left plus the `i^(th)` row of `lambda^T` minus the boxes from the top minus `1` for the box in the top-left corner
`mu_i = lambda_i-(i-1) + lambda_i^T - (i-1) - 1`
`= 2lambda_i - 2i + 1`
Claim: `mu_1 gt mu_2 gt ...`
`mu_i = 2lambda_i - 2i + 1`
`mu_(i+1) = 2lambda_(i+1) - 2(i+1) + 1`
Since `lambda` is a partition, `lambda_i ge lambda_(i+1)`
So
`mu_i = 2lambda_i - 2i + 1`
`ge 2lambda_(i+1)-2i-1 = mu_(i+1)`
Twelvefold Way
The twelvefold way considers all the ways to put `k` balls into `n` boxes. Putting balls into boxes can be thought of as a function `f:[k] rarr [n]`.
The balls and boxes can be distinguishable or indistinguishable. If the balls are distinguishable, each of them has a different color. If the balls are indistinguishable, they all have the same color. If the boxes are distinguishable, each box is labeled with a different number.
The function can be arbitrary, injective, or surjective. If the function is arbitrary, then there are no restrictions on which balls can go in which box. If the function is injective, then each box can have at most one ball (no box can have two or more balls). If the function is surjective, then each box has to have at least one ball.
Considering all the possible combinations, we get the following table:
| balls/boxes | `f` arbitrary | `f` injective | `f` surjective |
| distinguishable/distinguishable | `(1)` | `(2)` | `(3)` |
| indistinguishable/distinguishable | `(4)` | `(5)` | `(6)` |
| distinguishable/indistinguishable | `(7)` | `(8)` | `(9)` |
| indistinguishable/indistinguishable | `(10)` | `(11)` | `(12)` |
If the balls are distinguishable, then it is important to know which ball goes where. If the balls are indistinguishable, then we only need to know how many balls are in each box.
`(1)`: balls and boxes are distinguishable; `f` is arbitrary
For each of the `k` balls, there are `n` choices for which box it can be put in
So there are `n^k` ways
`(2)`: balls and boxes are distinguishable; `f` is injective
For the first ball, there are `n` choices of boxes
For the second ball, there are `n-1` choices of boxes
`vdots`
For the `k^(th)` ball, there is `(n-k+1)` choices of boxes
So there are `(n)_k = n(n-1)(n-2)...(n-k+1)` ways
`(3)`: balls and boxes are distinguishable; `f` is surjective
Some boxes might have one ball. Some boxes might have more than one ball. But none of them are empty
This is like breaking up `[k]` into `n` blocks
The number of ways to do this are counted by the number of set partitions of `[k]` into `n` blocks, which is `S(k,n)`
Since the boxes are distinguishable, the order of the partitions matter
So there are `n!S(k,n)` ways
`(4)`: balls are indistinguishable, boxes are distinguishable; `f` is arbitrary
Since the balls are indistinguishable, we're not concerned with which balls go to which box. We only need to know how many balls are in each box
Let `a_i` be the number of balls in box `i`
Then `a_1 + a_2 + ... a_n = k` where each `a_i ge 0`
This is a weak composition of `k` into `n` parts
So there are `((k+n-1),(k))` ways
`(5)`: balls are indistinguishable, boxes are distinguishable; `f` is injective
Since the balls are indistinguishable, we're not concerned with which balls go to which box. We only need to know how many balls are in each box
Additionally, since each box can only get at most one ball, we only need to know which box gets a ball
This is like choosing a subset of `k` boxes that get a ball
So there are `((n),(k))` ways
`(6)`: balls are indistinguishable, boxes are distinguishable; `f` is surjective
Since the balls are indistinguishable, we're not concerned with which balls go to which box. We only need to know how many balls are in each box
Let `a_i` be the number of balls in box `i`
Then `a_1 + a_2 + ... a_n = k` where each `a_i gt 0` since each box must have a ball
This is a composition of `k` into `n` parts
So there are `((k-1),(n-1))` ways
`(7)`: balls are distinguishable, boxes are indistinguishable; `f` is arbitrary
Some boxes might have one ball. Some boxes might have more than one ball. Some boxes might be empty
This is like breaking up `[k]` into at most `n` blocks, since each box might not have a ball
So there are `sum_(i=1)^nS(k,i)` ways
`(8)`: balls are distinguishable, boxes are indistinguishable; `f` is injective
Since the boxes are indistinguishable, we can rearrange the boxes in any order
Therefore, it doesn't matter where the balls go (putting the same ball in different boxes doesn't count as a separate ordering because we can just rearrange the boxes)
So there's really only one way to do this
However, since each box can have at most one ball, if there are more balls than boxes, then it is impossible
So the number of ways is `{(1\ if k le n),(0\ if k gt n):}`
`(9)`: balls are distinguishable, boxes are indistinguishable; `f` is surjective
Some boxes might have one ball. Some boxes might have more than one ball. But none of them are empty
This is like breaking up `[k]` into exactly `n` blocks, since each box must have a ball
The number of ways to do this are counted by the number of set partitions of `[k]` into `n` blocks, which is `S(k,n)`
So there are `S(k,n)` ways
`(10)`: balls and boxes are indistinguishable; `f` is arbitrary
Since the balls are indistinguishable, we're not concerned with which balls go to which box. We only need to know how many balls are in each box
Since the boxes are indistinguishable, we can rearrange them after we put the balls in them so that they're in decreasing order (with respect to the number of balls in each box)
This is like integer partitions of `k` into at most `n` parts, since each box might not have a ball
So there are `sum_(i=1)^np_i(k)` ways
`(11)`: balls and boxes are indistinguishable; `f` is injective
Since the boxes are indistinguishable, we can rearrange the boxes in any order
Therefore, it doesn't matter where the balls go (it doesn't matter anyway since the balls are indistinguishable)
So there's really only one way to do this
However, since each box can have at most one ball, if there are more balls than boxes, then it is impossible
So the number of ways is `{(1\ if k le n),(0\ if k gt n):}`
`(12)`: balls and boxes are indistinguishable; `f` is surjective
Since the balls are indistinguishable, we're not concerned with which balls go to which box. We only need to know how many balls are in each box
Since the boxes are indistinguishable, we can rearrange them after we put the balls in them so that they're in decreasing order (with respect to the number of balls in each box)
This is like integer partitions of `k` into exactly `n` parts, since each box must have a ball
So there are `p_n(k)` ways
So the twelvefold way table looks like:
| balls/boxes | `f` arbitrary | `f` injective | `f` surjective |
| distinguishable/distinguishable | `n^k` | `(n)_k` | `n!S(k,n)` |
| indistinguishable/distinguishable | `((k+n-1),(k))` | `((n),(k))` | `((k-1),(n-1))` |
| distinguishable/indistinguishable | `sum_(i=1)^nS(k,i)` | `{(1\ if k le n),(0\ if k gt n):}` | `S(k,n)` |
| indistinguishable/indistinguishable | `sum_(i=1)^np_i(k)` | `{(1\ if k le n),(0\ if k gt n):}` | `p_n(k)` |
Binomial Theorem
The binomial theorem provides a formula for expanding powers of `x+y`.
Theorem: `(x+y)^n = sum_(i=0)^n ((n),(i)) x^iy^(n-i)` for `n ge 0`
Consider the expansion `(x+y)^n = ubrace((x+y)(x+y)...(x+y))_n`
Multiply the terms, considering all the possible choices in each set of parentheses
Some terms will be repeated. For example, `x*x*x*...*x*y` and `x*x*y*x*...*x` both have `n-1` `x's` and `1` `y`
The number of repeated terms is the number of ways to create a term that has that form
The form of each term will be `i` `x's` and `n-i` `y's`
Which gives us `((n),(i))` ways to create `x^iy^(n-i)`
To get the final answer, we sum up all the possible products
The sum goes from `0` to `n` because we have situations where `x` appears `0` times and `x` appears `n` times
There are several identities that can be obtained by substituting values for `x` and `y`.
Let `x=y=1`
Then we get `2^n = sum_(i=0)^n ((n),(i))`, which was proven earlier
Let `x=-1`, `y=1`
Then we get `0 = sum_(i=0)^n (-1)^i((n),(i))`
There's an interesting result when we expand the sum:
`((n),(0))-((n),(1))+((n),(2))-((n),(3))+...+(-1)^n((n),(n)) = 0`
`((n),(0))+((n),(2))+... = ((n),(1))+((n),(3))+...`
`sum_(i text( even)) ((n),(i)) = sum_(i text( odd)) ((n),(i))`
This means the number of subsets with even size equals the number of subsets with odd size
So there are `(2^n)/2 = 2^(n-1)` subsets with even size (and likewise for subsets with odd size)
We can also obtain another identity by taking the derivative.
Applying `del/(delx)`, we get
`n(x+y)^(n-1) = sum_(i=0)^n i ((n),(i))x^(i-1)y^(n-i)`
`= sum_(i=1)^n i ((n),(i)) x^(i-1)y^(n-i)`
Setting `x=y=1`, we get
`n2^(n-1)=sum_(i=1)^n i ((n),(i))`
The right-hand side counts the number of ways to pick a subset `S` of `[n]` and an element `x` in that subset:
`|{(x,S)|S sube [n], x in S}|`
First, pick a subset `S` of size `i`: `((n),(i))` ways to to this
Then, pick an element `x` in `S`: `i` ways to to this
This is like picking members to be in a group, then picking a leader
The left-hand side tells a similar story
First, pick an element `x` to put in the subset `S`: `n` ways to do this
Then, pick the remaining elements to put in the subset `S`: `2^(n-1)` ways to do this
This is like picking a leader, then the group members
Multinomial Theorem
The multinomial theorem is a generalization of the binomial theorem.
For `n,k ge 0`,
`(x_1+x_2+...+x_k)^n = sum_(((a_1,a_2,...,a_k))) ((n),((a_1, a_2, ..., a_k))) x_1^(a_1)x_2^(a_2)...x_k^(a_k)`
where `a_i ge 0` and `a_1 + ... + a_k = n`
The proof is similar to the proof for the binomial theorem
The number of times `x_1^(a_1)x_2^(a_2)...x_k^(a_k)` appears is equal to the number of ways to choose each `x_i` exactly `a_i` times, which is `((n),((a_1,a_2,...,a_k)))`
Example: `(x_1+x_2+x_3)^3`
`= ((3),((3,0,0)))x_1^3 + ((3),((0,3,0)))x_2^3 + ((3),((0,0,3)))x_3^3`
`+ ((3),((2,1,0)))x_1^2x_2 + ((3),((2,0,1)))x_1^2x_3 + ((3),((1,2,0)))x_1x_2^2`
`+ ((3),((0,2,1)))x_2^2x_3 + ((3),((1,0,2)))x_1x_3^2 + ((3),((0,1,2)))x_2x_3^2`
`+ ((3),((1,1,1)))x_1x_2x_3`
`= x_1^3+x_2^3+x_3^3+3x_1^2x_2+3x_1^2x_3+3x_1x_2^2+3x_2^2x_3+3x_1x_3^2+3x_2x_3^2+6x_1x_2x_3`
`k^n = sum_(((a_1,...,a_k))) ((n),((a_1,...,a_k)))`
Set `x_1 = x_2 = ... = x_k = 1`
`0 = sum_(((a_1,...,a_k))) (1-k)^(a_1) ((n),((a_1,...,a_k)))`
Set `x_1 = 1-k`, `x_2 = ... = x_k = 1`
`nk^(n-1) = sum_(((a_1,...,a_k))) a_1 ((n),((a_1,...,a_k)))`
Apply `del/(delx_1)` and set `x_1 = ... = x_k = 1`
Formal Power Series
A formal power series is a way to encode a sequence of numbers as an algebraic object. The numbers are the coefficients of some (infinite) polynomial.
A formal power series (in variable `x`) is an expression of the form `sum_(n=0)^(oo) a_nx^n = A(x)` where `a_n` are scalars
Alternatively, it can be written as `sum_(n ge 0) a_nx^n`
Let `[x^n]A(x) = a_n` be the coefficient of `x^n`
Some special cases of formal power series are polynomials and scalars. Polynomials are formal power series where all the terms after a certain point are zero. Scalars are formal power series where `a_0` is a scalar and the rest of the terms are zero.
Two power series are equal if and only if all of their coefficients match
`A(x) = B(x)` if and only if `[x^n]A(x) = a_n = b_n = [x^n]B(x)` for all `n`
Addition and Multiplication of Formal Power Series
Let `A(x) = sum_(n ge 0) a_nx^n` and `B(x) = sum_(n ge 0) b_nx^n`
The sum of two formal power series is
`A(x)+B(x) = sum_(n ge 0) (a_n+b_n)x^n`
The product of two formal power series is
`A(x)B(x) = sum_(n ge 0) c_nx^n` where `c_n = sum_(i=0)^n a_ib_(n-i)`
(the indices have to add up to `n`)
Addition and multiplication are both commutative
`A(x)+B(x) = B(x)+A(x)`
`A(x)B(x) = B(x)A(x)`
and associative
`A(x)+[B(x)+C(x)] = [A(x)+B(x)]+C(x)`
`A(x)[B(x)C(x)] = [A(x)B(x)]C(x)`
Example: Let `A(x) = B(x) = sum_(n ge 0) x^n`
`A(x)+B(x) = sum_(n ge 0) 2x^n`
`A(x)B(x) = sum_(n ge 0) (n+1)x^n`
In the multiplication, `c_n = sum_(i=0)^n a_ib_(n-i) = sum_(i=0)^n 1 = n+1`
Invertibility of Formal Power Series
`A(x)` is invertible if there exists `B(x)` such that `A(x)B(x) = 1`
Then `B(x) = A(x)^(-1) = 1/(A(x))`
An example of an invertible formal power series:
Let `A(x) = sum_(n ge 0) x^n`, `B(x) = 1-x`
`A(x)B(x) = sum_(n ge 0) c_nx^n` where `c_n = sum_(i=0)^n a_ib_(n-i)`
If `n=0`, then `c_0 = a_0b_0 = 1`
If `n=1`, then `c_1 = a_0b_1 + a_1b_0 = (1)(-1) + (1)(1) = 0`
If `n ge 2`, then `c_n = 0` since `B(x)` has no degree `ge 2` term
So `c_n = 1` when `n=0` and `c_n = 0` when `n gt 0` `implies A(x)B(x) = sum_(n ge 0) c_nx^n = 1`
This means `sum_(n ge 0) x^n` is invertible with inverse `1-x`
We can also see that their product is equal to `1` by manually multiplying them:
`(1+x+x^2+x^3+...)(1-x)`
`= 1+x+x^2+x^3+...`
`\ \ \ \ \ \ \ \ -x-x^2-x^3-...`
`= 1`
From this result, we get an identity:
`(sum_(n ge 0) x^n)(1-x) = 1`
`sum_(n ge 0) x^n = 1/(1-x)`
Theorem: `A(x)` is invertible if and only if `[x^0]A(x) != 0`
A formal power series is invertible if and only if the constant term is nonzero
`(lArr)`Suppose `[x^0]A(x) != 0`. Want to show `A(x)` is invertible
Consider `B(x) = sum_(n ge 0) b_nx^n` and try to pick `b_n` so that `A(x)B(x) = 1`
Expanding out the equation `A(x)B(x) = 1` and matching coefficients, we get:
`a_0b_0 = 1`
`(a_1b_0 + a_0b_1)x = 0x`
`(a_2b_0 + a_1b_1 + a_0b_2)x^2 = 0x^2`
`vdots`
Using this system of equations, we can try to find `b_n`
`a_0b_0 = 1 implies b_0 = 1/a_0`
`a_1b_0+a_0b_1 = 0 implies b_1 = -(a_1b_0)/a_0 = -a_1/(a_0)^2`
`a_2b_0+a_1b_1+a_0b_2 = 0 implies b_2 = -(a_2b_0+a_1b_1)/a_0`
`vdots`
At each stage, it is possible to find `b_(n+1)` since it is in terms of `b_0,...,b_n`. More formally, we can do so using induction. Suppose we have solved for `b_0, ..., b_n`. At each stage, we have
`a_(n+1)b_0 + ... + a_0b_(n+1) = 0`
So we can solve for `b_(n+1) = -(a_(n+1)b_0 + ...)/a_0`
`(implies)`If the constant term is `0`, then the equation `a_0b_0 = 1` has no solution `implies` cannot find `b_n` `implies` `A(x)` is not invertible
Intuitively, if a formal power series has no constant term, then its product with any other power series will always be a sum of powers of `x`, which can never be equal to `1`
Composition of Formal Power Series
Let `A(x),B(x)` be formal power series such that `[x^0]A(x) = 0`
The composition `(B circ A)(x) = B(A(x))` is defined by `sum_(n ge 0) b_nA(x)^n`
It looks like we're taking the sum of infinitely many things, so how is this operation well defined, i.e., how are we going to get an answer if it looks like we're adding infinitely many things?
Since `A(x)` has no constant term, we have
`A(x) = a_1x + a_2x^2 + ...`
What happens when we take powers of `A(x)`? For `A(x)^2`, there is no constant term. There is also no linear term
`A(x)^2 = a_1^2x^2 + 2a_2a_1x^3 + ...`
Claim: `[x^i]A(x)^n = 0` for `i lt n`
Expanding `sum_(n ge 0) b_nA(x)^n`, we get
`b_0 + b_1A(x) + b_2A(x)^2 + b_3A(x)^3 + ...`
`= b_0`
`+ b_1a_1x + b_1a_2x^2 + b_1a_3x^3 + ...`
`+ b_2a_1^2x^2 + b_2 2a_2a_1x^3 + ...`
To get the coefficient of `x^n`, we only have to do a finite amount of additions. For example,
The coefficient of `x^0` is `b_0`
The coefficient of `x^1` is `b_1a_1x`
The coefficient of `x^2` is `b_1a_2x^2 + b_2a_1^2x^2`
So we will get an answer from doing this operation
If `A(x)` had a constant term, then we would end up having to do an infinite amount of additions
Example: Let `A(x) = x^d` where `d gt 0` and `B(x) = sum_(n ge 0) x^n`
`B(A(x)) = sum_(n ge 0) (x^d)^n = sum_(n ge 0) x^(dn)`
We can substitute this into the identity `(1-x)sum_(n ge 0) x^n = 1` to get a new identity:
`(1-x^d)sum_(n ge 0) x^(dn) = 1`
`1/(1-x^d) = sum_(n ge 0) x^(dn)`
Derivative of Formal Power Series
The derivative of `A`, written as `DA` or `A'`, is defined by `sum_(n ge 1) na_nx^(n-1) = sum_(n ge 0) (n+1)a_(n+1)x^n`
The familiar rules for derivatives apply to formal power series as well
`D(A+B) = DA + DB`
`D(A*B) = (DA)*B + A*(DB)` (product rule)
`D(B circ A) = (DA)(DB circ A)` (chain rule)
`D(A^(-1)) = -(DA)/A^2`
`D(A^n) = n(DA)A^(n-1)`
From before, `1/(1-x) = sum_(n ge 0) x^n`. We can use this identity to get a new identity by taking the derivative:
`1/(1-x)^2 = sum_(n ge 1) nx^(n-1) = sum_(n ge 0) (n+1)x^n`
It is possible to simplify `sum_(n ge 0) nx^n`:
`sum_(n ge 0) nx^n = sum_(n ge 1)nx^n = x sum_(n ge 1) nx^(n-1)` (we can pull out an `x` because there's no constant term)
`= x sum_(n ge 0) (n+1)x^n`
`= x*1/(1-x)^2`
`= x/(1-x)^2`
or
`sum_(n ge 0) nx^n = sum_(n ge 0) (n+1)x^n - sum_(n ge 0) x^n`
`= 1/(1-x)^2 - 1/(1-x)`
`= (1-(1-x))/(1-x)^2`
`= x/(1-x)^2`
In either case, we get the identity
`(1-x)^2 sum_(n ge 0) nx^n = x`
`sum_(n ge 0) nx^n = x/(1-x)^2`
Binomial Theorem (General)
The previous binomial theorem only considered nonnegative powers. Here, we consider real-numbered powers.
Let `m` be a real number and `k ge 0` be an integer
`((m),(0))=1`
`((m),(k)) = (m(m-1)(m-2)...(m-k+1))/(k!)`
Theorem: `(1+x)^m = sum_(n ge 0) ((m),(n)) x^n`
Consider `-1` as a power: `m=-1`
From before,
`1/(1-x) = sum_(n ge 0) x^n`
Substituting `-x` for `x`,
`1/(1+x) = sum_(n ge 0) (-x)^n = sum_(n ge 0) (-1)^nx^n`
Using the binomial theorem, we should get the same result
From the binomial theorem: `(1+x)^(-1) = sum_(n ge 0) ((-1),(n))x^n`
`((-1),(n)) = ((-1)(-2)(-3)...(-1-n+1))/(n!)`
`= ((-1)^n n!)/(n!)`
`= (-1)^n`
So the equation obtained from the binomial theorem matches the one from the formal power series
Consider any negative power: `m=-d` where `d gt 0` is an integer
We could try to see what it evaluates to without using the binomial theorem, but it gets pretty complicated
`(1+x)^(-d) = (1/(1+x))^d`
`= (sum_(n ge 0) (-1)^nx^n)^d`
Using the binomial theorem: `(1+x)^(-d) = sum_(n ge 0) ((-d),(n)) x^n`
`((-d),(n)) = ((-d)(-d-1)(-d-2)...(-d-n+1))/(n!)`
`= (-1)^n((d)(d+1)(d+2)...(d+n-1))/(n!)`
`= (-1)^n((d-1)!(d)(d+1)...(d+n-1))/((d-1)!n!)`
`= (-1)^n((d+n-1)!)/((d-1)!n!)`
`= (-1)^n((d+n-1),(n))`
So `(1+x)^(-d) = 1/(1+x)^d = sum_(n ge 0) (-1)^n((d+n-1),(n))x^n`
If we substitute `-x` for `x`, we get
`(1-x)^(-d) = 1/(1-x)^d = sum_(n ge 0) (-1)^n((d+n-1),(n))(-x)^n = sum_(n ge 0) ((d+n-1),(n))x^n`
Consider a fractional power: `m=1/2`
`(1+x)^(1/2)` is a formal power series whose square is `(1+x)`
Using the binomial theorem: `(1+x)^(1/2) = sum_(n ge 0) ((1/2),(n))x^n`
`((1/2),(n)) = ((1/2)(-1/2)(-3/2)...(-1/2-n+1))/(n!)`
`= (-1)^(n-1)((1/2)(1/2)(3/2)(5/2)...((2n-1)/2))/(n!)`
`= (-1)^(n-1)(3*5*7*...*2n-1)/(2^n n!)`
which doesn't really simplify further (unless we introduce the double factorial)
However, this means we've found the square root of a formal power series
`(sum_(n ge 0) ((1/2),(n))x^n)^2 = 1+x`
Given a quadratic equation, `A(x)t^2+B(x)t+C(x) = 0` where `A(x),B(x),C(x)` are formal power series, the solutions `t` are given by the quadratic formula
`t = (-B(x) +- sqrt(B(x)^2-4A(x)C(x)))/(2A(x))`
if `A(x)` is invertible
Ordinary Generating Functions
Ordinary generating functions are a way to encode a sequence of numbers as a formal power series.
Given a sequence of numbers `a_0, a_1, a_2, ...`, the ordinary generating function (ogf) is
`A(x) = sum_(n ge 0) a_nx^n`
Linear Recurrence Relations
We can use ordinary generating functions to find closed formulas for linear recurrence relations.
A sequence `a_0,a_1,...` satisfies a linear recurrence relation (of order `d`) if there exist scalars `c_1, c_2, ..., c_d` such that `c_d != 0` and for all `n ge d`
`a_n = c_1a_(n-1)+c_2a_(n-2)+...+c_da_(n-d)`
`d` is the minimum number of initial conditions that must be specified in order to find `a_n`
An example of a linear recurrence relation is the Fibonacci numbers
`1,1,2,3,5,8,13,21,...`
The relation is `a_n = a_(n-1)+a_(n-2)` for `n ge 2`
It satisifes a linear recurrence relation of order `2` where `c_1=c_2=1`
We have a recurrence relation for `a_n`, but it would be nice to find a closed formula for `a_n` so we could calculate `a_n` directly without going through the recurrence.
Consider the case when `d=1`
Then we have `a_n = c_1a_(n-1)` for `n ge 1`
`a_1=c_1a_0`
`a_2=c_1a_1=c_1^2a_0`
`a_3=c_1a_2=c_1^3a_0`
`vdots`
`a_n=c_1^na_0`
Here, `a_0` is an initial condition
Consider the case when `d=2`
Then we have `a_n = c_1a_(n-1)+c_2a_(n-2)` for `n ge 2` and `c_2 != 0`
The characteristic polynomial of this recurrence relation is defined to be
`t^2-c_1t-c_2`
The roots `r_1,r_2` are given by
`(c_1 +- sqrt(c_1^2+4c_2))/2`
So the characteristic polynomial can be factored as
`t^2-c_1t-c_2 = (t-r_1)(t-r_2)`
Theorem: If `r_1 != r_2`, then there are constants `alpha_1,alpha_2` such that `a_n = alpha_1r_1^n+alpha_2r_2^n` for all `n`
Given `a_0, a_1, ...`, create the ordinary generating function `A(x) = sum_(n ge 0)a_nx^n`
We can rewrite `A(x)` as
`a_0 + a_1x + sum_(n ge 2)a_nx^n`
The recurrence is only valid for `n ge 2` so we have to take out the first two terms in order to make the substitution below
From the definition of a linear recurrence relation, `a_n = c_1a_(n-1)+c_2a_(n-2)`, so
`A(x) = a_0 + a_1x + sum_(n ge 2)(c_1a_(n-1)+c_2a_(n-2))x^n`
`= a_0 + a_1x + c_1sum_(n ge 2)a_(n-1)x^n+c_2sum_(n ge 2)a_(n-2)x^n`
The last two summations are almost the same as `A(x)`:
`sum_(n ge 2)a_(n-1)x^n=xsum_(n ge 2)a_(n-1)x^(n-1)=x(a_1x+a_2x^2+a_3x^3+...)=x(A(x)-a_0)`
`sum_(n ge 2)a_(n-2)x^n=x^2sum_(n ge 2)a_(n-2)x^(n-2)=x^2sum_(n ge 0)a_nx^n=x^2A(x)`
Plugging these two back into `A(x)`, we get
`A(x) = a_0+a_1x+c_1x(A(x)-a_0)+c_2x^2A(x)`
`= a_0+a_1x+c_1xA(x)-c_1a_0x+c_2x^2A(x)`
Now we gather all the `A(x)`'s onto one side:
`A(x)-c_1xA(x)-c_2x^2A(x)=a_0+a_1x-a_0c_1x`
`A(x)(1-c_1x-c_2x^2)=a_0+a_1x-a_0c_1x`
We can divide both sides by `(1-c_1x-c_2x^2)` since it is invertible (because there is a constant term):
`A(x)=(a_0+a_1x-a_0c_1x)/(1-c_1x-c_2x^2)`
We can factor the bottom by using `t^2-c_1t-c_2 = (t-r_1)(t-r_2)` and plugging in `1/x` for `t`:
`x^(-2)-c_1x^(-1)-x_2=(1/x-r_1)(1/x-r_2)`
To make it look like `1-c_1x-c_2x^2`, we multiply by `x^2`:
`1-c_1x-c_2x^2=(1-r_1x)(1-r_2x)`
Knowing that the denominator can be factored, we can use partial fraction decomposition to get
`A(x)=(a_0+a_1x-a_0c_1x)/(1-c_1x-c_2x^2)=alpha_1/(1-r_1x)+alpha_2/(1-r_2x)`
for some constants `alpha_1,alpha_2`
Both of those terms are geometric series `color(red)(text(*))`, so we can write
`A(x)=alpha_1/(1-r_1x)+alpha_2/(1-r_2x)=alpha_1sum_(n ge 0)(r_1x)^n+alpha_2sum_(n ge 0)(r_2x)^n`
`= alpha_1sum_(n ge 0) r_1^nx^n + alpha_2sum_(n ge 0) r_2^nx^n`
The coefficient of `x^n` on the left-hand side is `a_n`
The coefficient of `x^n` on the right-hand side is `alpha_1r_1^n+alpha_2r_2^n`
So `a_n = alpha_1r_1^n+alpha_2r_2^n`
`color(red)(text(*))`this also comes from the identity `1/(1-x) = sum_(n ge 0)x^n`
To solve for `alpha_1,alpha_2`, plug in `n=0,1`
`a_0=alpha_1+alpha_2`
`a_1=alpha_1r_1+alpha_2r_2`
(`a_0` and `a_1` are part of the numbers in the sequence that is given)
This theorem can be seen with the Fibonacci numbers
They are defined by `a_n = a_(n-1)+a_(n-2)`, so the characteristic polynomial is `t^2-t-1`
The roots are `r_1 = (1+sqrt(5))/2` and `r_2 = (1-sqrt(5))/2`
According to the theorem, there exist `alpha_1, alpha_2` such that `a_n = alpha_1((1+sqrt(5))/2)^n+alpha_2((1-sqrt(5))/2)^n`
To find `alpha_1,alpha_2`, plug in `n=0,1`
`1=alpha_1+alpha_2`
`1=alpha_1((1+sqrt(5))/2)+alpha_2((1-sqrt(5))/2)`
Solving this system of equations, we get
`alpha_1=(1+sqrt(5))/(2sqrt(5))`
`alpha_2=-(1-sqrt(5))/(2sqrt(5))`
So `a_n = (1+sqrt(5))/(2sqrt(5))((1+sqrt(5))/2)^n-(1-sqrt(5))/(2sqrt(5))((1-sqrt(5))/2)^n`
`= 1/sqrt(5)((1+sqrt(5))/2)^(n+1)-1/sqrt(5)((1-sqrt(5))/2)^(n+1)`
Theorem: If `r_1=r_2`, then there are constants `alpha_1,alpha_2` such that `a_n = alpha_1r_1^n+nalpha_2r_1^n`
The proof is the same up until partial fraction decomposition
At that point, we have
`A(x) = alpha_1/(1-r_1x)+alpha_2/(1-r_1x)^2`
`alpha_1/(1-r_1x)` is a geometric series so that simplifies to `alpha_1sum_(n ge 0)r_1^nx^n color(red)(text(*))`
`alpha_2/(1-r_1x)^2` is the square of a geometric series so that simplifies to `alpha_2sum_(n ge 0)(n+1)r_1^nx^n color(red)(text(**))`
Comparing the coefficients of `x^n`, we get
`a_n = alpha_1r_1^n + alpha_2(n+1)r_1^n`
`= (alpha_1+alpha_2)r_1^n + alpha_2nr_1^n`
`color(red)(text(*))`this also comes from the identity `1/(1-x) = sum_(n ge 0)x^n`
`color(red)(text(**))`this also comes from the identity `1/(1-x)^2 = sum_(n ge 0)(n+1)x^n`
So the procedure for finding closed formulas for a linear recurrence relation of order `2` is:
- Form the characteristic polynomial and find its roots
- If the roots are the same, use `a_n = alpha_1r_1^n + alpha_2r_2^n`
- If the roots are the different, use `a_n = alpha_1r_1^n + nalpha_2r_1^n`
For general `d`, we have
`a_n=c_1a_(n-1)+c_2a_(n-2)+...+c_da_(n-d)` for `n ge d`
The characteristic polynomial is
`t^d-c_1t^(d-1)-c_2t^(d-2)-...-c_d = (t-r_1)(t-r_2)...(t-r_d)`
If all `r_1,r_2,...,r_d` are different, then there exist constants `alpha_1,alpha_2,...,alpha_d` such that
`a_n=alpha_1r_1^n+alpha_2r_2^n+...+alpha_dr_d^n`
What if some roots are the same?
Example: `d=5`, `r_1=r_2=r_3`, `r_4=r_5`, `r_1 != r_4`
Then there exist constants `alpha_1,alpha_2,alpha_3,alpha_4,alpha_5` such that
`a_n=alpha_1r_1^n+nalpha_2r_1^n+n^2alpha_3r_1^n+alpha_4r_4^n+nalpha_5r_4^n`
Combinatorial Interpretation
Ordinary generating functions sometimes make counting things easier.
We can think of `a_n` as counting the number of "structures" on the set `[n]`.
If `a_n = n!`, then `a_n` is the number of ways to order the elements in `[n]`
If `b_n = 2^n`, then `b_n` is the number of ways to pick a subset of `[n]`
`A(x)=sum_(n ge 0) a_nx^n` is an ogf encoding the number of orderings
`B(x)=sum_(n ge 0) b_nx^n` is an ogf encoding the number of subsets
In general, `a_n` is the number of ways of putting structure `alpha` on the set `[n]` and `b_n` is the number of ways of putting structure `beta` on the set `[n]`.
So `a_n+b_n` is the number of ways of putting structure `alpha` on the set `[n]` or putting structure `beta` on the set `[n]`. `(A+B)(x)` is an ogf encoding the number of ways of putting either `alpha` on `[n]` or `beta` on `[n]`.
In the above example, `a_n+b_n=n!+2^n` is the number of ways to pick either an ordering of the elements of `[n]` or a subset of `[n]`
`a_n+a_n=(2n)!` can be thought of as the number of ways of letting either person `1` order the elements of `[n]` or person `2` order the elements of `[n]`
The product is putting two structures on the elements of `[n]` simultaneously.
`A(x)B(x) = sum_(n ge 0) c_nx^n` where `c_n = sum_(i=0)^n a_ib_(n-i)`
`c_n=a_ib_(n-i)` is the number of ways to put structure `alpha` on `{1,...,i}` and to put structure `beta` on `{i+1,...,n}`
So `c_n` is the number of ways of splitting `[n]` into two consecutive pieces and putting `alpha` on the first piece and putting `beta` on the second piece
Example: A class has `n` days. We want to split the course into two portions, where the first portion is theory and the second portion is labs. One of the theory lectures is given by a guest lecturer and two of the lab days are carried out by the guest lecturer. How many ways are there to design the course?
Let `alpha` be picking the theory portion, `beta` be picking the lab portion
So `a_i = i` is the number of ways to pick one theory day out of `i` days to be the guest speaker
And `b_j = ((j),(2))` is the number of ways to pick two lab days out of `j` days to be the guest speaker
In terms of generating functions, we have
`A(x) = sum_(n ge 0)a_nx^n = sum_(n ge 0)nx^n = x/(1-x)^2`
`B(x) = sum_(n ge 0)b_nx^n = sum_(n ge 0)((n),(2))x^n = x^2/(1-x)^3 color(red)(text(*))`
`C(x) = A(x)B(x) = (x/(1-x)^2)(x^2/(1-x)^3) = x^3/(1-x)^5`
The coefficients of `C(x)` will be the answer to this question
`sum_(n ge 0) c_nx^n = x^3/(1-x)^5`
To do that, we can use the binomial theorem:
`x^3 sum_(n ge 0) ((-5),(n))x^n`
`= x^3 sum_(n ge 0) ((n+4),(n))x^n`
`= sum_(n ge 0) ((n+4),(n))x^(n+3)`
We want the coefficient of `x_n`, so we plug in `n-3`:
`= sum_(n ge 0) ((n+1),(n-3))x^n`
So `c_n = ((n+1),(n-3))`
`color(red)(text(*))`To get this identity, we expand `((n),(2))`:
`sum_(n ge 0) ((n),(2))x^n = sum_(n ge 0) (n(n-1))/2x^n`
`= 1/2 sum_(n ge 0) n(n-1)x^n`
We can find a formula for that by taking the derivative of `sum_(n ge 0)x^n = 1/(1-x)` twice and then multiplying by `x^2/2`:
`sum_(n ge 0)x^n = 1/(1-x)`
`sum_(n ge 0)nx^(n-1) = 1/(1-x)^2`
`sum_(n ge 0)n(n-1)x^(n-2) = 2/(1-x)^3`
`x^2/2sum_(n ge 0)n(n-1)x^(n-2) = x^2/2 2/(1-x)^3`
`1/2sum_(n ge 0)n(n-1)x^n = x^2/(1-x)^3`
We can get this answer without using generating functions
We can determine the class structure by knowing
- the day that the guest speaker speaks for the theory portion
- the last day of the theory portion
- the first day that the guest speaker leads the lab portion
- the second day that the guest speaker leads the lab portion
Let `a,b,c,d in [n]` be the days that these occur
Day `1` can be a day for the guest speaker
`1 le a`
The last day of the theory portion can be any day after the guest speaker (including day `1`)
`1 le a le b`
The first day that the guest speaker leads the lab portion cannot be day `1`
`1 le a le b lt c`
The second day that the guest speaker leads the lab has to be different from the first
`1 le a le b lt c lt d`
The second day that the guest speaker leads the lab can be the last day of the class
`1 le a le b lt c lt d le n`
This is the same situation as
`0 le a lt b lt c lt d le n`
So the problem becomes choosing `4` numbers from `n+1` numbers, which is `((n+1),(4))`
Note that `((n+1),(n-3)) = ((n+1),(n+1-n+3)) = ((n+1),(4))`
Example: Let `p_(le k)(n)` be the number of integer partitions of `n` using `le k` parts
Note: After taking the transpose, `p_(le k)(n)` is also the number of integer partitions of `n` where all parts are `le k`
We want a simple formula for `sum_(n ge 0) p_(le k)(n)x^n`
For `k=1`, it is the number of partitions where all parts are `le 1`. To do this, we just repeat `1` `n` times
`p_(le 1)(n) = 1` for all `n`
So the generating function is
`sum_(n ge 0) p_(le 1)(n)x^n = sum_(n ge 0)x^n = 1/(1-x)`
For `k=2`, it is the number of partitions using only `1`'s and `2`'s. This is the same as splitting `[n]` into two consecutive pieces, and then splitting the first piece into consecutive pieces of size `1` and splitting the second piece into consecutive pieces of size `2`
Example: `7 = 1+1+1+2+2`
The first piece is `1|2|3` and the second piece is `4\ 5|6\ 7`
Let `alpha` be breaking up a set into singletons, `beta` be breaking up a set into consecutive `2`-element subsets
Let `a_n` be the number of ways to do `alpha` to `[n]`, `b_n` be the number of ways to do `beta` to `[n]`
There's only one way to split a set into singletons, so `a_n = 1`
To split a set into consecutive `2`-element subsets, `n` has to be even. If it is, then there is one way to to do this, so `b_n = {(1 text( if n even)),(0 text( if n odd)):}`
The product of the generating functions will give us what we want:
`sum_(n ge 0) p_(le 2)(n)x^n = (sum_(n ge 0)a_nx^n)(sum_(n ge 0)b_nx^n)`
`= (sum_(n ge 0)x^n)(sum_(n ge 0)x^(2n))`
`= 1/(1-x)*1/(1-x^2)`
`= 1/((1-x)(1-x^2))`
Another way to see how `sum_(n ge 0)p_(le 2)(n)x^n = 1/((1-x)(1-x^2))`:
`1/((1-x)(1-x^2)) = (1+x+x^2+x^3+...)(1+x^2+x^4+x^6+...)`
`= (1+x^1+x^(1+1)+x^(1+1+1)+...)(1+x^2+x^(2+2)+x^(2+2+2)+...)`
Multiplying these two expressions, we get the following table:
| `1` | `x^1` | `x^(1+1)` | `x^(1+1+1)` | |
| `1` | `1` | `x^1` | `x^(1+1)` | `x^(1+1+1)` |
| `x^2` | `x^2` | `x^(1+2)` | `x^(1+1+2)` | `x^(1+1+1+2)` |
| `x^(2+2)` | `x^(2+2)` | `x^(1+2+2)` | `x^(1+1+2+2)` | `x^(1+1+1+2+2)` |
| `x^(2+2+2)` | `x^(2+2+2)` | `x^(1+2+2+2)` | `x^(1+1+2+2+2)` | `x^(1+1+1+2+2+2)` |
The result is that the exponents are partitions where are parts are `le 2`. The coefficient of `x^n` is the number of partitions of `n` where all parts are `le k`, i.e., `p_(le k)(n)`
For `k=3`, we have
`sum_(n ge 0) p_(le 3)(n)x^n = 1/((1-x)(1-x^2)(1-x^3))`
For general `k`, we have
`sum_(n ge 0) p_(le k)(n)x^n = 1/(1-x)*1/(1-x^2)*...*1/(1-x^k)`
`= prod_(i=1)^k 1/(1-x^i)`
Taking `k rarr oo`, we get
`p_(le oo)(n) = p(n)`
which is the number of partitions of `n` where all parts are `le oo`, which is the same as the number of partitions of `n`
So we have
`sum_(n ge 0)p(n)x^n = prod_(i=1)^(oo) 1/(1-x^i) = 1/((1-x)(1-x^2)(1-x^3)...)`
It looks like we're taking the product of infinitely many things. So how is this well defined, i.e., how do we get an answer? Expanding the product, we get
`1/((1-x)(1-x^2)(1-x^3)...) = (1+x+x^2+x^3+...)(1+x^2+x^4+x^6+...)(1+x^3+x^6+x^9+...)`
To multiply it all out, we choose one term from each set of parentheses and multiply all the terms together. We do this for all powers of `x`
For `x^0`, we're forced to pick all `1`'s from each set of parentheses so the product will be `1`
For `x^1`, we have to pick one `x` from the first set of parentheses and `1`'s from the rest
For `x^2`, we have to pick an `x^2` from a set of parentheses and `1`'s from the rest
For `x^3`, we have to pick an `x^3` or `x` and `x^2` and `1`'s from the rest
This process repeats infinitely, but each step only requires a finite amount of multiplications to calculate the coefficient of `x^n`
Example: Let `p_(text(odd))(n)` be the number of partitions of `n` where all parts are odd and let `p_(text(dist))(n)` be the number of partitions of `n` where all parts are distinct
| `n` | `p_(text(odd))(n)` | `p_(text(dist))(n)` |
| `1` | `(1)` | `(1)` |
| `2` | `(1,1)` | `(2)` |
| `3` | `(3)`,`(1,1,1)` | `(3)`,`(2,1)` |
| `4` | `(3,1)`,`(1,1,1,1)` | `(4)`,`(3,1)` |
| `5` | `(5)`,`(3,1,1)`,`(1,1,1,1,1)` | `(5)`,`(4,1)`,`(3,2)` |
We can use generating functions to show that these two are the same number
Theorem: `p_(text(odd))(n)` = `p_(text(dist))(n)`
Using generating functions, the goal is to show that `sum_(n ge 0)p_(text(odd))(n)x^n = sum_(n ge 0)p_(text(dist))(n)x^n`
From the previous example, we have
`sum_(n ge 0)p_(text(odd))(n)x^n = (1/(1-x))(1/(1-x^3))(1/(1-x^5))...`
For `p_(text(dist))(n)x^n`, we can only use unique exponents, so we have
`sum_(n ge 0)p_(text(dist))(n)x^n = (1+x)(1+x^2)(1+x^3)(1+x^4)...`
`1+x^k` can be rewritten as
`1+x^k = (1-x^(2k))/(1-x^k)`
So `p_(text(dist))(n)x^n` can be rewritten as
`sum_(n ge 0)p_(text(dist))(n)x^n = (1-x^2)/(1-x)*(1-x^4)/(1-x^2)*(1-x^6)/(1-x^3)*(1-x^8)/(1-x^4)*...`
All the terms in the numerator will cancel out the terms in the denominator with even exponents. What's left is the odd terms
`= 1/(1-x)*1/(1-x^3)*1/(1-x^5)*...`
`= sum_(n ge 0)p_(text(odd))(n)x^n`
Composition of Ordinary Generating Functions
We compose ordinary generating functions when we want to break up `[n]` into consecutive intervals, apply a structure on each interval, and then apply another structure on a set of those intervals.
`a_n` is the number of ways to apply structure `alpha` on a set of size `n` and `a_0=0`. `h_n` is the number of ways to break `[n]` into consecutive intervals and place structure `alpha` on each interval. The generating functions are `A(x) = sum_(n ge 0) a_nx^n` and `H(x) = sum_(n ge 0) h_nx^n`.
Theorem: `H(x) = 1/(1-A(x))`
`A(x)^k` is the ordinary generating function for the number of ways to break up `[n]` into `k` consecutive intervals and place structure `alpha` on each piece
This is counted by `h_n` when we sum over all `k`
So `H(x) = sum_(k ge 0) A(x)^k = 1/(1-A(x))`
Example: There are `n` soldiers in a line and we want to split the line at several places to form teams of soldiers. Also, we want to assign a leader to each team. How many ways are there to do this?
Let `a_n` be the number of ways to pick a leader from `n` people. Then `a_n = n`
`A(x) = sum_(n ge 0) a_nx^n = sum_(n ge 0)nx^n = x/(1-x)^2`
The answer is given by `h_n`
`H(x) = 1/(1-A(x)) = 1/(1-x/(1-x)^2)`
`= (1-x)^2/((1-x)^2-x)`
`= (1-2x+x^2)/(1-3x+x^2)`
Using partial fractions, we get
`h_n = 1/sqrt(5)((3+sqrt(5))/2)^n-1/sqrt(5)((3-sqrt(5))/2)^n`
So far, we broke `[n]` into consecutive intervals and applied a structure to each interval. We could apply another structure `beta` on a subset of those intervals.
`b_n` is the number of structures of type `beta` on a set of size `n`. The generating function is `B(x) = sum_(n ge 0) b_nx^n`. Now `h_n` is the number of ways to break `[n]` into consecutive intervals, place structure `alpha` on each interval, then place structure `beta` on a subset of those intervals.
Theorem: `H(x) = B(A(x))`
`b_kA(x)^k` is the ordinary generating function for the number of ways to break up `[n]` into `k` consecutive intervals, place structure `alpha` on each piece, and then place structure `beta` on the `k` pieces
This is counted by `h_n` when we sum over all `k`
So `H(x) = sum_(k ge 0) b_kA(x)^k = B(A(x))`
Going back to the soldier example, suppose we want to additionally pick some of the teams for night duty. How many ways are there to do this?
Let `b_n` be the number of ways to pick some teams for night duty. This is the same as picking a subset, so `b_n = 2^n`
`B(x) = sum_(n ge 0) b_nx^n = sum_(n ge 0) 2^nx^n = sum_(n ge 0) (2x)^n = 1/(1-2x)`
From before, `A(x) = x/(1-x)^2`
The number of ways to do this is counted by `h_n`
`H(x) = B(A(x)) = 1/(1-(2x)/(1-x)^2)`
`= (1-x)^2/((1-x)^2-2x)`
`= (1-2x+x^2)/(1-4x+x^2)`
Using partial fractions, we would get our answer
We could get the answer without using generating functions
Each soldier could be
- the first soldier on a team for night duty
- the first soldier on a team not assigned to night duty
- not the first soldier on a team
The only exception is the first soldier who only has two choices
So there are two choices for the first soldier and three choices for the rest of the `n-1` soldiers
The number of ways is `2*3^(n-1)`
Catalan Numbers
Catalan numbers can be used to count a lot of things. One way to view them is the number of ways to balance `n` pairs of parentheses.
Let `C_n` be the number of ways to write a balanced expression using `n` pairs of parentheses
For example, for `n=3`
`()()()`
`(())()`
`((()))`
`(()())`
`()(())`
`C_n` is also the same as the number of words with `n` left parentheses and `n` right parentheses such that every initial segment has at least as many `(` as `)`
`C_n` is also the same as the number of sequences of `n` counts of `+1`'s and `n` counts of `-1`'s such that every initial partial sum is `ge 0`
There is some kind of recursive structure to these parentheses. For example, we can have a balanced pair of parentheses and put another pair of balanced parentheses inside. We can use this recursive structure to obtain a recurrence relation. It turns out that the recurrence relation will be nonlinear.
Lemma: If `n ge 0`, then `C_n = sum_(i = 0)^(n-1)C_iC_(n-1-i)`
Every expression starts with a `(` and is matched by some `)`
In between those `()`, we can put another set of balanced parentheses
- Let `i` be the number of pairs inside
- We can put up to `n-1` pairs of parentheses inside
- Then there are `C_i` choices for `0 le i le n-1`
After the `)`, we can put another set of balanced parentheses
- After putting `i` pairs inside the initial balanced parentheses, we have `n-(i+1) = n-1-i` pairs leftover
- Then there are `C_(n-1-i)` choices
These choices are independent of each other, so there are `C_iC_(n-1-i)` total choices
Since `i` can go from `0` to `n-1`, we have `sum_(i = 0)^(n-1)C_iC_(n-1-i)`
So we have a recurrence relation for the Catalan numbers. Now we can try to find a closed formula for `C_n` using generating functions. In this case, we can define the generating function `C(x) = sum_(n ge 0) C_nx^n` where `C_0 = 1`.
We start by multiplying both sides of the recurrence relation by `x^n`
`C_nx^n = sum_(i = 0)^(n-1)C_iC_(n-1-i)x^n`
And then summing over all positive `n`
`sum_(n gt 0)C_nx^n = sum_(n gt 0) sum_(i = 0)^(n-1)C_iC_(n-1-i)x^n`
The left-hand side is `C(x)` without the `n=0` term (which is `C_0 = 1`), so the left-hand side evaluates to `C(x)-1`
The right-hand side looks like the result of multiplying two generating functions
`C(x)^2 = sum_(n ge 0) (sum_(i=0)^nC_iC_(n-i))x^n` by the definition of multiplying two generating functions
`sum_(n gt 0) sum_(i = 0)^(n-1)C_iC_(n-1-i)x^n` almost looks like `C(x)^2`. We can manipulate it so that it does
Since `n gt 0`, we can pull out an `x` from `C(x)^2`
`x sum_(n gt 0) sum_(i=0)^(n-1)C_iC_(n-1-i)x^(n-1)`
Then we can re-index to get
`x sum_(n ge 0) sum_(i=0)^n C_iC_(n-i)x^n`
`= xC(x)^2`
So the right-hand side evaluates to `xC(x)^2`
Which gives us
`C(x)-1=xC(x)^2`
`xC(x)^2-C(x)+1=0`
This tells us that `C(x)` is a solution to a quadratic equation `xt^2-t+1=0`. We can use the quadratic formula to solve for `t = C(x)`, which gives us
`t = (1 +- sqrt(1-4x))/(2x)`
There are two possibilities for `t = C(x)`:
- `C(x) = (1 + sqrt(1-4x))/(2x) implies 2xC(x) = 1 + sqrt(1-4x)`
- `C(x) = (1 - sqrt(1-4x))/(2x) implies 2xC(x) = 1 - sqrt(1-4x)`
There's only one correct choice for `C(x)`, so which one do we pick? Looking at `2xC(x)`, whatever `C(x)` is, when we multiply it with `2x`, there will be no constant term. So `1+sqrt(1-4x)` must not have a constant term either
The constant term of `1+sqrt(1-4x)` is `1` plus whatever the constant term of `sqrt(1-4x)` is, which we can find by using the binomial theorem:
`(1-4x)^(1/2) = sum_(n ge 0) ((1/2),(n)) (-4x)^n`
The constant term appears when `n=0`, so `((1/2),(0))=1` is the constant term
- The constant term of `1 + sqrt(1-4x)` is `2`
- The constant term of `1 - sqrt(1-4x)` is `0`
So `C(x) = (1-sqrt(1-4x))/(2x)`
Alternatively, looking at `2xC(x) = 1-sqrt(1-4x)`, if we plug in `x=0` on the left-hand side, we get `0`. So plugging in `x=0` on the right-hand side should give us `0` too
`1+sqrt(1-4*0)`
`= 1+sqrt(1)`
`= 1+1 = 2`
`1-sqrt(1-4*0)`
`= 1-sqrt(1)`
`= 1-1 = 0`
So we pick the expression with the negative sign
To simplify this, we can use the binomial theorem (again):
`(1-4x)^(1/2) = sum_(n ge 0) ((1/2),(n))(-4x)^n`
We can simplify this by expanding `((1/2),(n))`:
`((1/2),(n)) = ((1/2)(-1/2)(-3/2)...(1/2-n+1))/(n!)`
So we have
`sum_(n ge 0) ((1/2),(n))(-4x)^n = sum_(n ge 0) ((1/2)(-1/2)(-3/2)...(1/2-n+1))/(n!) (-4)^n x^n`
`= sum_(n ge 0) (1/2)^n (1(-1)(-3)...(1-2n+2))/(n!) (-4)^n x^n`
`= sum_(n ge 0) (-2)^n (1(-1)(-3)...(-2n+3))/(n!) x^n`
`= -sum_(n ge 0) 2^n (1*1*3*...*(2n-3))/(n!) x^n`
`= -sum_(n ge 0) 2^n (1*1*3*...*(2n-3))/(n!) * (2*4*6*...*(2n-2))/(2*4*6*...*(2n-2)) x^n`
`= -sum_(n ge 0) 2^n ((2n-2)!)/(n!) * 1/(2*4*6*...*(2n-2)) x^n`
`= -sum_(n ge 0) 2 ((2n-2)!)/(n!) * 1/(1*2*3*...*(n-1)) x^n`
`= -2sum_(n ge 0) ((2n-2)!)/(n!(n-1)!) x^n`
So `(1-4x)^(1/2) = -2sum_(n ge 0) ((2n-2)!)/(n!(n-1)!) x^n`
Since we're looking for `C(x)`,
`C(x) = (1-(1-4x)^(1/2))/(2x)`
`= 1/(2x)(1-(1-4x)^(1/2))`
`= 1/(2x)(1+2sum_(n ge 0) ((2n-2)!)/(n!(n-1)!) x^n)`
`= 1/(2x)(1-1+2sum_(n ge 1) ((2n-2)!)/(n!(n-1)!) x^n)` (taking out the constant term)
`= sum_(n ge 1) ((2n-2)!)/(n!(n-1)!) x^(n-1)`
`= sum_(n ge 1) ((2(n-1))!)/(n!(n-1)!) x^(n-1)`
`= sum_(n ge 0) ((2n)!)/((n+1)!n!) x^n`
So `C(x) = sum_(n ge 0) ((2n)!)/((n+1)!n!) x^n` and `C_n = ((2n)!)/((n+1)!n!)`, which looks like a binomial coefficient after pulling out `1/(n+1)`:
`C_n = 1/(n+1)((2n)!)/(n!n!)`
`= 1/(n+1)((2n),(n))`
Other Catalan objects for `n=3`
1) The number of ways to apply binary operation `text(*)` to `n+1` inputs
`a text(*) (b text(*) (c text(*) d))`
`a text(*) ((b text(*) c) text(*) d)`
`(a text(*) b) text(*) (c text(*) d)`
`((a text(*) b) text(*) c) text(*) d`
`(a text(*) (b text(*) c)) text(*) d`
(Look at 2) first)
Let `alpha_n` be the number of ways to apply binary operation `text(*)` to `n+1` inputs
There's a bijection between 1) and 2)
Place a `text(*)` inside each node
From the bottom, combine leaves into one expression with `text(*)`
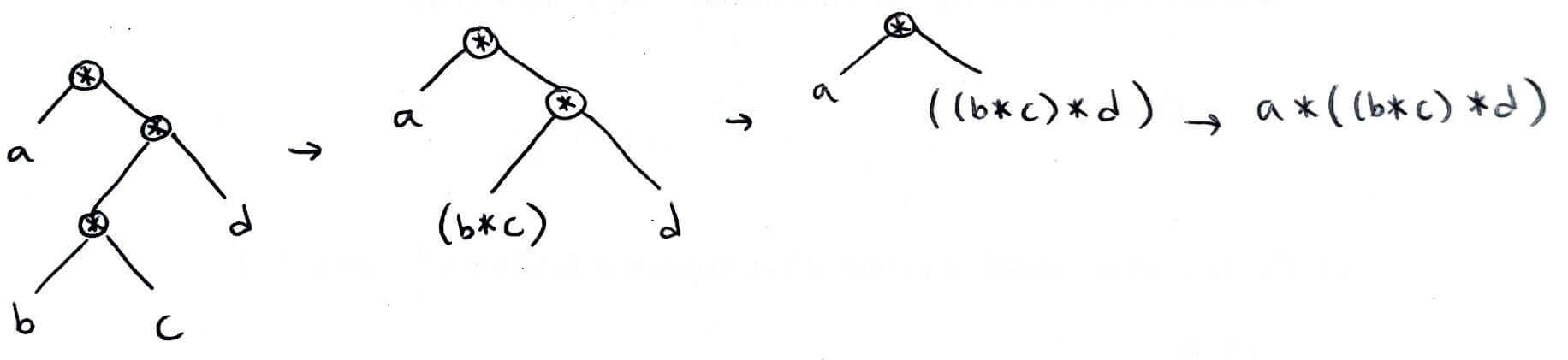
To go the other way, start with the outermost `text(*)` and make that the root
Make the left and right part subtrees
So `alpha_n = beta_n = C_n`
2) The number of rooted binary trees with `n+1` leaves

Let `beta_n` be the number of ways to form a rooted binary tree with `n+1` leaves
Remove the root to form two trees (left and right)
The left part has `i` leaves, so there are `beta_(i-1)` ways to do this
The right part has `n+1-i` leaves, so there are `beta_(n-i)` ways to do this
The left part needs to have at least one leaf and the right part also needs to have at least one leaf, so `1 le i le n`
`beta_n = sum_(i=1)^n beta_(i-1)beta_(n-i) = sum_(i=0)^(n-1)beta_ibeta_(n-1-i)`
So `beta_n` satisifies the same recurrence as the Catalan numbers
3) The number of forward paths from `(0,0)` to `(n,n)` which do not go above the line `x=y`

Let `gamma_n` be the number of forward paths from `(0,0)` to `(n,n)` which do not go above the line `x=y`
There is a bijection between 3) and the Catalan numbers
A right step corresponds to a `(` and a step up corresponds to a `)`
So `gamma_n = C_n`
The forward paths also satisify the recurrence relation
Given a path, let `i` be the smallest positive value such that `(i,i)` is on `x=y`
Chop the path into two pieces
The first piece is the path from `(0,0)` to `(i,i)` which does not touch `x=y` except at the endpoints
- If we remove the first and last steps, we end up with the path `(1,0)` to `(i,i-1)` which does not go above `x=y+1`
- If we shift by `(-1,0)`, we get a path from `(0,0)` to `(i-1,i-1)` not going above `x=y`, for which there are `gamma_(i-1)` paths
The second piece is the path from `(i,i)` to `(n,n)`
- This is the same as the path from `(0,0)` to `(n-i,n-i)`, for which there are `gamma_(n-i)` paths
So the total number of paths is `gamma_n = sum_(i=1)^ngamma_(i-1)gamma_(n-i) = sum_(i=0)^(n-1)gamma_(i)gamma_(n-1-i)`
`gamma_n` satisifies the same recurrence as the Catalan numbers
Exponential Generating Functions
Exponential generating functions are similar to ordinary generating functions. They're still formal power series, but they encode sequences differently. As such, the interpretations of operations, such as multiplication and composition, have different meanings and can be used for different applications of problems.
For example, when using ordinary generating functions, we were constrained to consecutive intervals. But it may be more natural to form groups where the elements are not consecutive. Exponential generating functions give us a way to do that.
Given a sequence `a_0, a_1, a_2, ...`, the exponential generating function (egf) is
`A(x) = sum_(n ge 0) a_n/(n!)x^n`
When `a_n=1` for all `n`, we use `e^x` to denote `sum_(n ge 0) 1/(n!)x^n`
Taking the derivative (bringing down an `n`) is like shifting the sequence by one
`A(x) = sum_(n ge 0) a_n/(n!)x^n`
`A(x) = a_0 + sum_(n ge 1) a_n/(n!)x^n`
`A'(x) = sum_(n ge 1) (na_n)/(n!)x^(n-1)`
`A'(x) = sum_(n ge 1) a_n/((n-1)!)x^(n-1)`
`A'(x) = sum_(n ge 0) a_(n+1)/(n!)x^n`
Example: Suppose we have a sequence defined by `a_0 = 1` and `a_n = n(a_(n-1)-n+2)` for `n ge 1`
Let's try to encode it as an ordinary generating function
So let `A(x) = sum_(n ge 0)a_nx^n` be the ogf
Multiplying the recurrence by `x^n` and summing over all `n ge 1`, we get
`sum_(n ge 1)a_nx^n = sum_(n ge 1)(na_(n-1)-n^2+2n)x^n`
`A(x)-a_0 = sum_(n ge 1)na_(n-1)x^n + sum_(n ge 1)(-n^2+2n)x^n`
`A(x)-a_0 = xsum_(n ge 1)na_(n-1)x^(n-1) + sum_(n ge 1)(-n^2+2n)x^n`
`A(x)-a_0 = xsum_(n ge 0)na_nx^n + sum_(n ge 1)(-n^2+2n)x^n`
`A(x)-a_0 = x^2A'(x) + sum_(n ge 1)(-n^2+2n)x^n`
Now we have a differential equation, which would be too complicated to deal with
Instead, let's try to encode this sequence as an exponential generating function
So let `A(x) = sum_(n ge 0) a_n/(n!)x^n` be the egf
We could substitute in the recurrence after changing the summation to `n ge 1` (by pulling out the constant term)
`A(x) = sum_(n ge 0)a_n/(n!)x^n`
`= a_0 + sum_(n ge 1)a_n/(n!)x^n`
`= 1 + sum_(n ge 1)(na_(n-1)-n(n-2))/(n!)x^n`
`= 1 + sum_(n ge 1)(na_(n-1))/(n!)x^n - sum_(n ge 1)(n(n-2))/(n!)x^n`
`= 1 + sum_(n ge 1)a_(n-1)/((n-1)!)x^n - sum_(n ge 1)(n-2)/((n-1)!)x^n`
`= 1 + xsum_(n ge 1)a_(n-1)/((n-1)!)x^(n-1) - xsum_(n ge 1)(n-2)/((n-1)!)x^(n-1)`
`= 1 + xsum_(n ge 0)a_n/(n!)x^n - xsum_(n ge 0)(n-1)/(n!)x^n`
`= 1 + xA(x) - xsum_(n ge 0)n/(n!)x^n + xsum_(n ge 0) 1/(n!)x^n`
`= 1 + xA(x) - xsum_(n ge 1)1/((n-1)!)x^n + xe^x`
`= 1 + xA(x) - x^2sum_(n ge 1)1/((n-1)!)x^(n-1) + xe^x`
`= 1 + xA(x) - x^2sum_(n ge 0)1/(n!)x^n + xe^x`
`= 1 + xA(x) - x^2e^x + xe^x`
So we have
`A(x) = 1 + xA(x) - x^2e^x + xe^x`
`A(x) - xA(x) = 1 - x^2e^x + xe^x`
`A(x)(1-x) = 1 - x^2e^x + xe^x`
`A(x) = (1 - x^2e^x + xe^x)/(1-x)`
`= 1/(1-x) + ((x-x^2)e^x)/(1-x)`
`= 1/(1-x) + (x(1-x)e^x)/(1-x)`
`= 1/(1-x) + xe^x`
`= sum_(n ge 0)x^n + xsum_(n ge 0)1/(n!)x^n`
`= sum_(n ge 0)x^n + sum_(n ge 0)1/(n!)x^(n+1)`
`= sum_(n ge 0)x^n + sum_(n ge 1)1/((n-1)!)x^n`
Normally for ordinary generating functions, we would get our answer `a_n` by looking at the coefficient of `x^n`. However, with exponential generating functions, we have `sum_(n ge 0)a_n/(n!)x^n`. So the summations have to be in that form before we can extract the coefficient
`= sum_(n ge 0)(n!)/(n!)x^n + sum_(n ge 1)n/(n!)x^n`
`= 1 + sum_(n ge 1)(n!)/(n!)x^n + sum_(n ge 1)n/(n!)x^n`
`= 1 + sum_(n ge 1)(n!+n)/(n!)x^n`
So `a_n = n!+n`
Product of Exponential Generating Functions
The product of two exponential generating functions can be thought of as putting a structure on a subset of `[n]` and putting another structure on the complement.
Let `alpha, beta` be structures on sets. Let `a_n` be the number of ways to do `alpha` on a set of size `n`. Let `b_n` be the number of ways to do `beta` on a set of size `n`. Let `c_n` be the number of ways to pick a subset `S sube [n]`, put `alpha` on `S` and put `beta` on `[n]\\S`.
Then `sum_(n ge 0)c_n/(n!)x^n = (sum_(n ge 0)a_n/(n!)x^n)(sum_(n ge 0)b_n/(n!)x^n)`.
More generally, we can handle more than two structures. If we had `k` structures, the product of their egf's is the egf for the number of ways to write `[n] = S_1 uu S_2 uu ... uu S_k` such that no subsets overlap and we put the `i^(th)` structure on `S_i`.
Let `A(x) = sum_(n ge 0)a_n/(n!)x^n` and `B(x) = sum_(n ge 0) b_n/(n!)x^n`
Lemma: `A(x)B(x) = sum_(n ge 0) c_n/(n!)x^n` where `c_n = sum_(i=0)^n ((n),(i)) a_ib_(n-i)`
The coefficient of `x^n` in `A(x)B(x)` is `sum_(i=0)^na_i/(i!)b_(n-i)/((n-i)!)` by the definition of multiplying two power series
But it is also equal to `c_n/(n!)`
`c_n/(n!) = sum_(i=0)^n(a_ib_(n-i))/(i!(n-i)!)`
`c_n = sum_(i=0)^n(n!a_ib_(n-i))/(i!(n-i)!)`
`c_n = sum_(i=0)^n((n),(i))a_ib_(n-i)`
Let `a_n` be the number of structures of type `alpha` on a set of size `n`
Let `b_n` be the number of structures of type `beta` on a set of size `n`
Then `((n),(i))a_ib_(n-i)` is the number of ways to pick a subset `S sube [n]` of size `i`, putting structure `alpha` on `S`, and putting structure `beta` on `[n]\\S`
So `c_n` is the number of ways to pick subsets (possibly empty) of `[n]`, putting structure `alpha` on `S`, and putting structure `beta` on `[n]\\S`
Example: There are `n` football players and we want to split them up into two groups. Both groups will be assigned an ordering, but the each player in the second group also gets to choose one of three colors for their uniforms. How many ways are there to do this?
Let `alpha` be the ways to order a set. So `a_n = n!`
Let `beta` be the ways to order a set and assign a color to each element. So `b_n = 3^n n!`
`A(x) = sum_(n ge 0)a_n/(n!)x^n = sum_(n ge 0)x^n = 1/(1-x)`
`B(x) = sum_(n ge 0)b_n/(n!)x^n = sum_(n ge 0)3^nx^n = 1/(1-3x)`
`C(x) = A(x)B(x) = 1/(1-x)*1/(1-3x)`
Using partial fractions, we get
`1/(1-x)*1/(1-3x) = (3/2)/(1-3x)-(1/2)/(1-x)`
`= 3/2sum_(n ge 0)3^nx^n - 1/2sum_(n ge 0)x^n`
`= 3/2sum_(n ge 0)(3^n n!)/(n!)x^n - 1/2sum_(n ge 0)(n!)/(n!)x^n`
So `c_n = 3/2 3^n n! - 1/2 n!`
There's a trick for getting rid of odd/even terms of a formal power series `A(x) = sum_(n ge 0)a_nx^n`
To get rid of all odd terms, add `A(-x)` and divide the sum by `2`:
`A(x)+A(-x) = sum_(n ge 0)a_nx^n + sum_(n ge 0)(-1)^na_nx^n`
When `n` is odd, the terms will cancel each other out, so there are only even terms leftover
When `n` is even, the terms will be added, so we need to divide by `2`
`(A(x)+A(-x))/2 = sum_(n ge 0)a_(2n)x^(2n)`
To get rid of all even terms, subtract `A(-x)` and divide the difference by `2`:
`A(x)-A(-x) = sum_(n ge 0)a_nx^n - sum_(n ge 0)(-1)^na_nx^n`
When `n` is even, the terms will cancel each other out, so there are only odd terms leftover
When `n` is odd, the terms will be added, so we need to divide by `2`
`(A(x)-A(-x))/2 = sum_(n ge 0)a_(2n+1)x^(2n+1)`
Example: There are `n` distinguishable telephone poles and we want to paint each of them either red or blue. But the number of blue poles must be even. How many ways are there to do this?
Let `R(x)` be the egf for painting `n` poles red. There's only one way to paint `n` poles red, so `R(x) = sum_(n ge 0)1/(n!)x^n = e^x`
Let `B(x)` be the egf for painting `n` poles blue. There's only one way to paint `n` poles blue if `n` is even and zero ways if `n` is odd, so `B(x) = sum_(n ge 0)1/((2n)!)x^(2n) = (e^x+e^(-x))/2`
`sum_(n ge 0)c_n/(n!)x^n = R(x)B(x) = e^x((e^x+e^(-x))/2)`
`= (e^(2x)+1)/2`
`= 1/2e^(2x) + 1/2`
`= 1/2 sum_(n ge 0) 1/(n!)(2x)^n + 1/2`
`= 1/2 sum_(n ge 0) 2^n/(n!)x^n + 1/2`
`= sum_(n ge 0) 2^(n-1)/(n!)x^n + 1/2`
`= 1 + sum_(n ge 1) 2^(n-1)/(n!)x^n`
So `c_0 = 1` and `c_n = 2^(n-1)`
We can get this answer without using generating functions
If we knew which poles were blue, then we automatically know which ones are red too
So all we need to do is pick a subset of even size of `n`
There are `2^(n-1)` subsets of even size of `n`
We can use the product of egf's to get an egf for the Stirling numbers.
Define `a_n=1` if `n ge 0` and `a_0=0`
We can interpret this as counting the number of ways for a set to be nonempty
`A(x) = sum_(n ge 0)a_n/(n!)x^n = sum_(n ge 1)x^n/(n!) = e^x-1`
`A(x)^2 = sum_(n ge 0)c_n/(n!)x^n`
`c_n` is the number of ways to pick a subset `S sube [n]` such that `S != O/` and `[n]\\S != O/`
The Stirling numbers, `S(n,k)`, counted the number of ways to break up a set of size `n` into `k` nonempty pieces without regard to order. In this case, `k=2` and the order matters. `S` is like the first subset and `[n]\\S` is like the second subset. So this is ordered set partitions with two blocks, the number of which is counted by `2!S(n,2)`
But `c_n` is also the number of ordered set partitions of `[n]` into `2` blocks. So `c_n = 2!S(n,2)`
Plugging that back into `A(x)^2`, we get
`A(x)^2 = sum_(n ge 0)c_n/(n!)x^n = sum_(n ge 0)(2!S(n,2))/(n!)x^n`
But `A(x)^2` is also equal to `(e^x-1)^2`, so we get
`sum_(n ge 0)(2!S(n,2))/(n!)x^n = (e^x-1)^2`
`(e^x-1)^2` is the exponential generating function for ordered set partitions into two blocks
Dividing by `2!`, we also get
`sum_(n ge 0)(S(n,2))/(n!)x^n = (e^x-1)^2/(2!)`
`(e^x-1)^2/(2!)` is the exponential generating function for set partitions into two blocks, i.e., `S(n,2)`
For general `k`, if we take `A(x)^k`, then that would be counting the number of ways to break `[n]` into `k` nonempty subsets, which is exactly the number of ordered set partitions into `k` blocks
So more generally,
`(e^x-1)^k = sum_(n ge 0)(k!S(n,k))/(n!)x^n`
`(e^x-1)^k/(k!) = sum_(n ge 0)(S(n,k))/(n!)x^n`
Using the exponential generating function for the Stirling numbers, we can also get one for the Bell numbers, `B(n) = sum_(k=0)^nS(n,k)`, which are the number of set partitions of `[n]`.
The exponential generating function would be `sum_(n ge 0)(B(n))/(n!)x^n`
`= sum_(n ge 0)1/(n!)[sum_(k ge 0)S(n,k)]x^n`
`= sum_(k ge 0)sum_(n ge 0)(S(n,k))/(n!)x^n`
`= sum_(k ge 0)(e^x-1)^k/(k!)`
`= e^(e^x-1)`
The advantage of having formulas like these is that it makes taking products much simpler when the formulas are nice and compact, possibly leading to simplifications. It's pretty hard to work with a bunch of summations.
While they are clean formulas, they are often difficult to work with, compared to the formulas obtained from ordinary generating functions, which are usually rational expressions that can be simplified by partial fraction decomposition and expressed as geometric series. Here, there's no easy way to see what the `n^(th)` coefficient of something like `e^(e^x-1)` is.
Compositions of Exponential Generating Functions
We compose exponential generating functions when we want to break up `[n]` into blocks, apply a structure on each block, and then apply another structure on a set of those blocks.
Let `alpha` be a structure on a set.
Let `a_n` be the number of ways to do `alpha` on a set of size `n` (assume `a_0=0`).
Define `h_n` to be the number of ways to pick a set partition on `[n]` into `k` blocks for some `k` and put structure `alpha` on each block.
The egf's are `A(x)=sum_(n ge 0)a_n/(n!)x^n` and `H(x) = sum_(n ge 0)h_n/(n!)x^n`.
Theorem: `H(x)=e^(A(x))`
`A(x)^k` is the egf for the number of ways to write `[n] = S_1 uu S_2 uu ... uu S_k` such that the `S_i`'s don't overlap and put structure `alpha` on each `S_i`
Since now the order doesn't matter, we divide by `k!` to get `(A(x)^k)/(k!)`
Considering all `k`, we get `H(x) = sum_(k ge 0) (A(x)^k)/(k!) = e^(A(x))`
Example: A bijection `f:S rarr S` is an involution if `f circ f = id_s`. Applying the function to one element twice results in the original element
Let `h_n` be the number of involutions of a set of size `n`
Find a formula for `H(x) = sum_(n ge 0)h_n/(n!)x^n`
Involutions are built out of two pieces:
- elements that go to themselves
- pairs of elements that get swapped
So we can think of involutions as set partitions of `[n]` into blocks of size `1` or `2`
- elements in the `1`-block are elements that go to themselves
- elements in the `2`-block are elements that get swapped
Let `alpha` be the structure where we apply the identity function on an element or swap two elements
Then `a_1=a_2=1` and `a_n=0` otherwise
`A(x) = sum_(n ge 0)a_n/(n!)x^n`
`= x + (x^2)/(2!)`
`H(x) = e^(A(x))`
`= e^(x+(x^2)/(2!))`
Example: Let `h_n` be the number of ways to split up `n` people into nonempty groups and have each sit in a circle
Find a formula for `H(x) = sum_(n ge 0)h_n/(n!)x^n`
Let `alpha` be the number of ways to circularly order a set
There are `n!` ways to order people in a circle, but `n` rotations will be the same ordering
So `a_n = (n!)/n = (n-1)!` and `a_0=0`
`A(x) = sum_(n ge 0)a_n/(n!)x^n`
`= sum_(n ge 1) ((n-1)!)/n!x^n`
`= sum_(n ge 1) (x^n)/n`
`= log(1/(1-x))`
`H(x) = e^(A(x))`
`= e^(log(1/(1-x)))`
`= 1/(1-x)`
In fact, we can actually find a formula for the `h_n`
`sum_(n ge 0)h_n/(n!)x^n = 1/(1-x) = sum_(n ge 0)x^n`
`h_n/(n!) = 1`
`h_n = n!`
After breaking up `[n]` into blocks and putting structure `alpha` on each block, we could take a set of those blocks and put another structure `beta` on a set of those blocks.
Let `beta` be a structure on a set. Let `b_n` be the number of ways to do `beta` on a set of size `n`. The generating function is `B(x) = sum_(n ge 0)b_n/(n!)x^n`.
Now let `h_n` be the number of ways to pick a set partition of `[n]`, put `alpha` on each block, and put `beta` on a set of blocks.
Theorem: `H(x) = B(A(x))`
This is the generalized version of the theorem `H(x) = e^(A(x))` where `B(x) = sum_(n ge 0)1/(n!)x^n = e^x` (all the `b_i`'s are `1`)
Lagrange Inversion
The Lagrange inversion formula is a technique for extracting coefficients from a formal power series that satisifies a certain identity.
Suppose `R(x) = sum_(n ge 0)r_n/(n!)x^n` satisfies `R(x) = xe^(R(x))`
It's difficult to isolate `R(x)` in this situation
One thing we could do is to solve for the coefficients one by one
`r_0 = 0` because there's no constant term in `xe^(R(x))`
This means that the lowest degree term of `R(x)` is `r_1x^1`, which means that the lowest degree term of `R(x)^n` is `r_1^nx^n`
Rewriting `R(x)=xe^(R(x))` we get
`R(x) = xsum_(n ge 0)1/(n!)R(x)^n`
`= x(1 + R(x) + (R(x)^2)/(2!) + (R(x)^3)/(3!) + ...)`
If we want to find `r_n`, then we only need to consider the first `n` terms, i.e., `x(1+R(x)+...+(R(x)^(n-1))/((n-1)!))`
By definition, `r_1=[x^1]R(x)=[x^1]xe^(R(x))`
From the observation above, we don't need to consider the whole summation; we only need to look at the first term
So `r_1 = [x^1](x(1)) = 1`
`r_2 = [x^2]R(x) = [x^2]e^(R(x))`
`= [x^2](x(1+R(x)))`
`= [x^2](x+xR(x))`
`= [x^2]x + [x^2]xR(x)`
`= 0 + [x^1]R(x)`
`= r_1 = 1`
`r_3 = [x^3]R(x) = [x^3]e^(R(x))`
`= [x^3](x(1+R(x)+(R(x)^2)/(2!)))`
`= [x^3](x+xR(x)+(xR(x)^2)/(2!))`
`= [x^3]x + [x^3]xR(x) + [x^3](xR(x)^2)/(2!)`
`= 0 + [x^2]R(x) + 1/2[x^2]R(x)^2`
`= 0 + r_2 + 1/2(r_0r_2 + r_1r_1 + r_2r_0)`
`= 1 + 1/2 = 3/2`
And we could repeat this process for the rest of the coefficients
The Lagrange inversion formula gives us a way to find the coefficient directly without computing previous coefficients.
Let `G(x)` be a formal power series with a nonzero constant term.
Suppose `A(x)` is a formal power series such that `A(x) = xG(A(x))`.
Theorem: `[x^n]A(x) = 1/n[x^(n-1)](G(x)^n)` for `n gt 0`
Going back to the previous example, we can let `G(x) = e^x` and `A(x) = R(x)`
By the theorem, `r_n = [x^n]R(x)`
`= 1/n[x^(n-1)]e^(nx)`
`= 1/n[x^(n-1)]sum_(k ge 0)1/(k!)(nx)^k`
`= 1/n(1/((n-1)!)n^(n-1))`
`= n^(n-1)/(n!)`
This formula agrees with the previous calculations
`r_1 = 1^0/(1!) = 1`
`r_2 = 2^1/(2!) = 1`
`r_3 = 3^2/(3!) = 9/6 = 3/2`
We can use the Lagrange inversion formula to get the formula for the Catalan numbers fairly easily.
Before, we showed that `C(x) = 1+xC(x)^2`
This isn't in the correct form to use the theorem because of the `1+`. (Also, if we were to use the theorem, then `C(x)` shouldn't have a constant term, but we know that `c_0=1`)
To fix these problems, we could subtract off the constant term
Define `A(x) = C(x)-1`. Now we could use the theorem on `A(x)`
Substituting the identity for `A(x)` we get
`A(x)+1 = 1+x(A(x)+1)^2`
`A(x) = x(A(x)+1)^2`
Let `G(x) = (x+1)^2`, which has a nonzero constant term `1`
So `A(x)=xG(A(x)) implies [x^n]A(x) = 1/n[x^(n-1)](G(x)^n) = 1/n[x^(n-1)](x+1)^(2n)`
`= 1/n[x^(n-1)]sum_(k ge 0)((2n),(k))x^k`
`= 1/n((2n),(n-1))`
`= 1/n((2n)!)/((n-1)!(n+1)!)`
`= ((2n)!)/(n!(n+1)!)`
`= ((2n)!)/(n!n!)1/(n+1)`
`= 1/(n+1)((2n),(n))`
This is the coefficient of `A(x)`, but what we're looking for is the coefficient of `C(x)`
Well the coefficients of `A(x)=C(x)-1` are the same as those for `C(x)` except for the constant term
So `[x^n]A(x) = [x^n]C(x)` for `n gt 0` `implies C_n = 1/(n+1)((2n),(n))`
We can generalize the Catalan numbers in a way that is compatible with the Lagrange inversion formula.
Before, we showed that `C_n` is the number of rooted binary trees with `n+1` leaves
We could generalize this so that `c_n` is the number of rooted `k`-ary trees with `n` internal vertices
Let `C(x) = sum_(n ge 0)c_nx^n` be the ordinary generating function for `c_n`
Removing the root, we get `k` smaller trees
Let `n_i` be the number of internal vertices of the `i^(th)` tree (`n_1+...+n_k=n-1`)
For this choice, there are `c_(n_1), c_(n_2), ..., c_(n_k)` possibilities
So `c_n = sum_(n_1+n_2+...n_k=n-1)c_(n_1)c_(n_2)...c_(n_k)` for `n ge 1`
This is a product of `k` generating functions so we get
`C(x) = 1+xC(x)^k`
To get `c_n`, we could use the Lagrange inversion formula
Let `A(x) = C(x)-1`
Then
`A(x)+1 = 1+x(A(x)+1)^k`
`A(x) = x(A(x)+1)^k`
Let `G(x) = (x+1)^k`
So `A(x)=xG(A(x)) implies [x^n]A(x) = 1/n[x^(n-1)](G(x)^n) = 1/n[x^(n-1)](x+1)^(kn)`
`= 1/n((kn),(n-1))`
The coefficients of `A(x)=C(x)-1` are the same as those for `C(x)` except for the constant term
So `[x^n]A(x) = [x^n]C(x)` for `n gt 0` `implies C_n = 1/(n)((kn),(n-1))`
Inclusion-Exclusion
Inclusion-exclusion is used to count the size of a set that is made up of smaller sets, which may overlap with each other. This means we have to make sure that we don't overcount elements.
Theorem: Let `A_1, A_2, ..., A_n` be finite sets. Then
`|A_1 uu A_2 uu ... uu A_n| = sum_(j=1)^n(-1)^(j-1)sum_(1 le i_1 lt i_2 ... lt i_j le n)|A_(i_1) nn A_(i_2) ... nn A_(i_j)|`
We want every `x in A_1 uu ... uu A_n` to be counted exactly once
Let `S = {s_1, s_2, ..., s_k}` be all the indices such that `x in A_(s_1), ..., A_(s_k)`
`x` is only going to be counted by `(-1)^(j-1)|A_(i_1) nn ... nn A_(i_j)|` when all the `i_1, i_2, ..., i_j` are in `S` (otherwise `x` doesn't belong in the intersection)
So we have to look at all the possible ways of choosing indices in `S`
The number of times `x` is counted is
`sum_(T sube S, T != O/) (-1)^(|T|-1) = sum_(i=1)^(|S|)((|S|),(i))(-1)^(i-1)`
We could simplify that by using the binomial theorem
When `x=-1,y=1` we get
`0 = (1-1)^n = sum_(i=0)^n((n),(i))(-1)^i`
`= 1+sum_(i=1)^n((n),(i))(-1)^i`
So we have `0 = 1+sum_(i=1)^n((n),(i))(-1)^i`
`-sum_(i=1)^n((n),(i))(-1)^i = 1`
`sum_(i=1)^n((n),(i))(-1)^(i-1) = 1`
which looks like the summation above
So the number of times `x` is counted is
`sum_(i=1)^(|S|)((|S|),(i))(-1)^(i-1)=1`
`j` represents how many sets we consider at a time
the inner sum looks at the number of ways to intersect `j` sets
Example: `n=2`
Starting with `j=1`, we take all possible subsets of size `1`:
`|A_1 uu A_2| = color(red)(|A_1|+|A_2|)`
Then when `j=2`, we take all possible subsets of size `2`:
`|A_1 uu A_2| = |A_1|+|A_2|color(red)(-|A_1 nn A_2|)`
Example: `n=4`
All possible subsets of size `1`:
`|A_1 uu A_2 uu A_3 uu A_4| = color(red)(|A_1|+|A_2|+|A_3|+|A_4|)`
All possible subsets of size `2`:
`|A_1 uu A_2 uu A_3 uu A_4| = |A_1|+|A_2|+|A_3|+|A_4|`
`color(red)(-|A_1 nn A_2| - |A_1 nn A_3| - |A_1 nn A_4| - |A_2 nn A_3| - |A_2 nn A_4| - |A_3 nn A_4|)`
All possible subsets of size `3`:
`|A_1 uu A_2 uu A_3 uu A_4| = |A_1|+|A_2|+|A_3|+|A_4|`
`-|A_1 nn A_2| - |A_1 nn A_3| - |A_1 nn A_4| - |A_2 nn A_3| - |A_2 nn A_4| - |A_3 nn A_4|`
`color(red)(+|A_1 nn A_2 nn A_3| + |A_1 nn A_2 nn A_4| + |A_1 nn A_3 nn A_4| + |A_2 nn A_3 nn A_4|)`
All possible subsets of size `4`:
`|A_1 uu A_2 uu A_3 uu A_4| = |A_1|+|A_2|+|A_3|+|A_4|`
`-|A_1 nn A_2| - |A_1 nn A_3| - |A_1 nn A_4| - |A_2 nn A_3| - |A_2 nn A_4| - |A_3 nn A_4|`
`+|A_1 nn A_2 nn A_3| + |A_1 nn A_2 nn A_4| + |A_1 nn A_3 nn A_4| + |A_2 nn A_3 nn A_4|`
`color(red)(-|A_1 nn A_2 nn A_3 nn A_4|)`
When proving things using inclusion-exclusion, we want to express our set as one that satisfies one of `n` conditions. Then each `A_i` is the set that only satisfies condition `i`. The union of all the `A_i`'s will be our original set.
A bijection `f:S rarr S` is a derangement if `f(s)!=s` for all `s in S`
Theorem: The number of derangements of a set of size `n` is `sum_(i=0)^n(-1)^i(n!)/(i!)`
It's easier to count the number of non-derangements and subtract from the total number of permutations
`f` is not a derangement if `f(1)=1` or `f(2)=2` or `...\ f(n) = n`
Let `A_i = {f:[n] rarr [n]|f(i)=i}`. So all the non-derangements are included in `A_1 uu A_2 uu ... uu A_n`
`A_1` is the set of all bijections such that `f(1)=1`. For `2,...,n` there are `(n-1)!` ways to assign values, so `|A_1|=(n-1)!`
By similar reasoning, `|A_2| = ... = |A_n| = (n-1)!`
`A_1 nn A_2` is the set of all bijections such that `f(1)=1` and `f(2)=2`. For `3,...,n` there are `(n-2)!` ways to assign values, so `|A_1 nn A_2| = (n-2)!`
In general, `|A_(i_1) nn ... nn A_(i_j)| = (n-j)!`
Since the union of all the `A_i`'s gives us the number of non-derangements, we can use inclusion-exclusion
`|A_1 uu ... uu A_n| = sum_(j=1)^n(-1)^(j-1)sum_(1 le i_1 lt ... lt i_j le n)|A_(i_1) nn ... nn A_(i_j)|`
`= sum_(j=1)^n(-1)^(j-1)sum_(1 le i_1 lt ... lt i_j le n)(n-j)!`
`= sum_(j=1)^n(-1)^(j-1)((n),(j))(n-j)!`
`= sum_(j=1)^n(-1)^(j-1)(n!)/(j!)`
The number of derangements is the number of permutations minus the number of non-derangements, which is
`n!-sum_(j=1)^n(-1)^(j-1)(n!)/(j!)`
`= n!+sum_(j=1)^n(-1)^j(n!)/(j!)`
`= sum_(j=0)^n(-1)^j(n!)/(j!)`
the last part can be seen as rewriting `n!` as `(n!)/(0!)`
Big idea: To be a non-derangement, it needs to satisfy (at least) one of `n` conditions. The set of non-derangements is the union of `n` simpler sets.
Formulas obtained from inclusion-exclusion will have alternating signs, which makes it hard to tell how big that quantity is. For example, is `sum_(i=0)^n(-1)^i(n!)/(i!)` a big or small number? It turns out that this specific formula (accidentally?) has another nice interpretation that can be obtained using calculus.
Example: What percentage of permutations are derangements?
The answer is the number of derangements divided by the number of permutations, which is
`1/(n!)sum_(j=0)^n(-1)^j(n!)/(j!)`
`= sum_(j=0)^n(-1)^j/(j!)`
From calculus,
`e^x = sum_(i ge 0)x^i/(i!)`
`e^x` converges everywhere, so if we plug in a number for `x`, that series will converge
Also, the larger `n` gets, the closer we get to the value. So even though it's an infinite sum, large enough `n` will provide a good enough approximation
Plugging in `x=-1`, we get
`e^(-1) = sum_(i ge 0)(-1)^i/(i!) ~~ sum_(i=0)^n(-1)^i/(i!)`
So the number of derangements is
`= sum_(j=0)^n(-1)^j/(j!) ~~ 1/e ~~ 0.367...`
In a room with a lot of people, if we throw everyone's hat into a pile and randomly give everyone a hat, there's about a `37%` chance that no one will get their own hat back
We can also use inclusion-exclusion to get a formula for the Stirling numbers. `S(n,k)` is the number of set partitions of `[n]` into `k` blocks. `k!S(n,k)` is the number of ordered set partitions of `[n]` into `k` blocks. It can also be thought of as the number of surjective functions from `[n]` to `[k]`.
Theorem: `S(n,k) = 1/(k!)sum_(i=0)^k(-1)^i((k),(i))(k-i)^n` for `n ge k gt 0`
Count the number of non-surjective functions from `[n]` to `[k]` and subtract from the total number of functions from `[n]` to `[k]`
Being non-surjective means `1` is not in the image or `2` is not in the image or `...\ k` is not in the image
Define `A_i = {f:[n] rarr [k]|i` is not in the image of `f}` for `1 le i le k`
Then the set of non-surjective functions is the union of the `A_i`'s
`A_1` is all the functions where `1` is not in the image, which is the same as `{`functions `[n] rarr {2,3,...,k}}`
There are `(k-1)^n` such functions, so `|A_1| = (k-1)^n`
By similar reasoning, `|A_i| = (k-1)^n` for all `i`
`A_1 nn A_2 = {`functions `[n] rarr {3,4,...,k}}` so `|A_1 nn A_2| = (k-2)^n`
In general, `|A_(i_1) nn ... nn A_(i_j)| = (k-j)^n`
The number of non-surjective functions is
`|A_1 uu ... uu A_k| = sum_(j=1)^k(-1)^(j-1)sum_(1 le i_1 lt ... lt i_j le k)|A_(i_1) nn ... nn A_(i_j)|`
`= sum_(j=1)^n(-1)^(j-1)sum_(1 le i_1 lt ... lt i_j le k)(k-j)^n`
`= sum_(j=1)^n(-1)^(j-1)((k),(j))(k-j)^n`
The number of surjective functions is the total number of functions minus the number of non-surjective functions, so we have
`k!S(n,k) = k^n - sum_(j=1)^k(-1)^(j-1)((k),(j))(k-j)^n`
`k!S(n,k) = k^n + sum_(j=1)^k(-1)^j((k),(j))(k-j)^n`
`k!S(n,k) = sum_(j=0)^k(-1)^j((k),(j))(k-j)^n`
To get the Stirling numbers, divide by `k!`:
`S(n,k) = 1/(k!)sum_(j=0)^k(-1)^j((k),(j))(k-j)^n`
Möbius Inversion
Möbius inversion deals with a different kind of overcounting. It usually shows up in number theory, but we can use it to count necklaces.
Let `A` be an alphabet of size `k`. We want to count the number of words of length `n` up to cyclic symmetry. The idea is that if we arrange the letters in a circle, each rotation would be considered the same word.
For example, `a_1a_2a_3a_4 -= a_4a_1a_2a_3 -= a_3a_4a_1a_2 -= a_2a_3a_4a_1`
Because of the cyclic symmetry, we have to divide out the commonalities to get the number of unique arrangements. It seems like the number of symmetries is equal to the number of times we can shift it to get the same word back.
One idea is to divide the number of words of length `n` by the length of the word.
`= k^n/n`
The problem with this idea is that not every word is overcounted equally.
For example, `a_1a_1a_1a_1` is not overcounted four times; it is only overcounted once
The number of symmetries is actually equal to the number of times we can shift it. It's just not always equal to the length of the word.
Given a word, its period is the least number of times we need to rotate it to get the original word back
Fact: the period always divides the length of the word
Let `omega(d)` be the number of words of period `d`
To count the number of necklaces, we can count the number of words with period `1, 2, ..., n`, dividing out the commonalities in each case.
`#\ text(necklaces) = sum_(d|n)(omega(d))/d`
The number of necklaces of length `4`
`= (omega(1))/1 + (omega(2))/2 + (omega(4))/4`
`= k + (k(k-1))/2 + (k^4-k-(k(k-1)))/4`
It's tempting to think that the number of words with period `4` is `n(n-1)(n-2)(n-3)`
But there are words with period `4` that don't have all distinct letters, such as `1312`
To count the number of words with period `4`, we count the total number of words of length `4` and subtract off words with period `1` and period `2`
If a word of length `4` doesn't have period `1` or period `2`, then it must have period `4`
This idea actually leads to another identity
The number of words of length `n` is the number of words with period `1, 2, ..., n`
`k^n = sum_(d|n)omega(d)`
This is valid for any `n`, so this gives us a system of equations we can use to solve for each `omega(d)`
For `n=4`:
`k^4 = omega(4)+omega(2)+omega(1)`
`k^2 = omega(2)+omega(1)`
`k^1 = omega(1)`
Which gives us
`omega(1) = k`
`omega(2) = k^2-omega(1) = k^2-k`
`omega(4) = k^4-omega(2)-omega(1) = k^4-k^2+k-k = k^4-k^2`
For `n=6`:
`k^6 = omega(6)+omega(3)+omega(2)+omega(1)`
`k^3 = omega(3)+omega(1)`
`k^2 = omega(2)+omega(1)`
`k^1 = omega(1)`
Which gives us
`omega(1) = k`
`omega(2) = k^2-omega(1) = k^2-k`
`omega(3) = k^3-omega(1) = k^3-k`
`omega(6) = k^6-omega(3)-omega(2)-omega(1) = k^6-k^3+k-k^2+k-k = k^6-k^3-k^2+k`
We could use this system of equations to manually solve for `omega(d)` and calculate the number of necklaces that way. But it would be nicer to find a pattern for `omega(d)` and solve for it directly.
For `n gt 1`, write `n` as a product of primes
The Möbius function is defined by
`mu(n) = {(0\ text(if n is divisible by a square of some prime)), ((-1)^k\ text(if n is a product of k different primes)):}`
and `mu(1)=1`
`mu(12) = mu(2^2*3) = 0`
`mu(30) = mu(2*3*5) = (-1)^3 = -1`
`mu(8) = mu(2^3) = 0`
Lemma: `sum_(d|n)mu(d) = 0` for `n gt 1`
Consider the prime factorization of `n = p_1^(a_1)p_2^(a_2)...p_r^(a_r)` where each `p_i` is distinct and all `a_i gt 0`
To get divisors of `n`, we just make the exponents smaller
So all divisors `d` of `n` are of the form `d = p_1^(b_1)p_2^(b_2)...p_r^(b_r)` where `0 le b_i le a_i`
We can rewrite the sum as
`sum_(d|n)mu(d) = sum_(0 le b_i le a_i)mu(p_1^(b_1)p_2^(b_2)...p_r^(b_r))`
By the Möbius function, if `n` is divisible by a prime more than once, then the result is `0`. So we only need to consider `b_i`'s `lt 2`:
`= sum_(0 le b_i le 1)mu(p_1^(b_1)p_2^(b_2)...p_r^(b_r))`
Since each `b_i` is either `0` or `1`, we either include each `p_i` or we don't:
`= sum_(S sube [r])mu(prod_(i in S)p_i)`
We have a product of distinct primes so the result will be `(-1)` to some power by the Möbius function:
`= sum_(S sube [r])(-1)^(|S|)`
`= sum_(j=0)^r (-1)^j((r),(j)) = 0`
by the binomial theorem with `x=-1,y=1`
Theorem: `omega(d) = sum_(e|d)mu(d/e)k^e` for any `d`
From the identity before, we can rewrite `k^e` as a sum of `omega`'s
`sum_(e|d)mu(d/e)k^e = sum_(e|d)mu(d/e)sum_(f|e)omega(f)`
We can rearrange the sum to get
`= sum_(f|d)(omega(f)sum_(e|d, e\ text(divisible by )f)mu(d/e))`
`= sum_(f|d)(omega(f)sum_(g|d/f)mu(g))color(red)(text(*))`
By the lemma, `sum_(g|d/f)mu(g) = 0` if `d/f gt 1 implies d gt f`
So we don't need to consider all the terms where `d gt f`. The only term left is when `f=d`:
`= omega(d)sum_(g|d/d)mu(g)`
`= omega(d)sum_(g|1)mu(g)`
`= omega(d)sum_(1)1`
`= omega(d)`
`color(red)(text(*))`We can define a function `varphi:{e|e\ ` divides `d` and `e` is divisible by `f} rarr {g|g` divides `d/f}` by `varphi(e)=d/e`
`varphi` is a bijection, so we can rewrite the sum
We could verify that this theorem is consistent with the previous examples for `d=4` and `d=6`
`omega(4) = mu(4/1)k^1 + mu(4/2)k^2 + mu(4/4)k^4`
`= mu(2^2)k^1 + mu(2)k^2 + mu(1)k^4`
`= -k^2 + k^4`
`omega(6) = mu(6/1)k^1 + mu(6/2)k^2 + mu(6/3)k^3 + mu(6/6)k^6`
`= mu(2*3)k^1 + mu(3)k^2 + mu(2)k^3 + mu(1)k^6`
`= k - k^2 - k^3 + k^6`
Counting necklaces is a specific case of Möbius inversion. Generally, we use Möbius inversion when we have a function that is a sum of another function, and we want to write it the other way around.
Theorem: Let `f,g` be functions defined on positive integers. Assume that `f(n) = sum_(d|n)g(d)` for all `n ge 1`
Then `g(d) = sum_(e|d)mu(d/e)f(e)` for all `d ge 1`
In the necklace problem, `f(n) = k^n` and `g(d) = omega(d)`
Practice Problems
Chapter 3
3.1: How many functions are there from `[n]` to `[n]` that are not one-to-one?
Count the number of functions that are one-to-one and subtract from the total number of functions
Total number of functions: there are `n` choices in the codomain for each element in the domain `implies n^n`
One-to-one: assign each element in the domain one element in the codomain and permute `implies n!`
`color(red)(n^n - n!)`
3.2: Prove that the number of subsets of `[n]` that have an odd number of elements is `2^(n-1)`
For each of the first `n-1` elements, there are `2` choices: in the subset or not in the subset `implies 2^(n-1)`
For the `n^(th)` element, there is only `1` choice:
- if there are an even number of elements in the subset so far, then add the `n^(th)` element in the subset
- if there are an odd number of elements in the subset so far, then don't add the `n^(th)` element in the subset
3.3: A company has `20` employees, `12` males and `8` females. How many ways are there to form a committee of `5` employees that contains at least one male and one female?
Count the number of committees that have all males and all females and subtract both from the total number of ways to form a committee
Total number of ways to form a committee: `((20),(5))`
All male: `((12),(5))`
All female: `((8),(5))`
`color(red)(((20),(5)) - ((12),(5)) - ((8),(5)))`
3.6: How many five-digit positive integers are there with middle digit `6` that are divisible by three?
This problem is the same as counting the number of four-digit positive integers divisible by three since `6` is divisible by three
There are `9999-1000+1 = 9000` four-digit positive integers
Every third number is divisible by three `implies 1/3` of the `9000` four-digit positive integers are divisible by three
`color(red)(3000)`
3.7: How many five-digit positive integers are there that contain the digit `9` and are divisible by three?
There are `99999-10000+1 = 90000` five-digit positive integers
Every third number is divisible by three `implies 1/3*90000 = 30000` five-digit positive integers are divisible by three
Now count how many of those don't contain a `9` and subtract from the total number of five-digit positive integers divisible by three
There are `8` choices for the first digit
There are `9` choices for the second digit
There are `9` choices for the third digit
There are `9` choices for the fourth digit
The fifth digit depends on what the first `4` digits sum up to
- if the sum mod `3` equals `0`, then the fifth digit can be `0`, `3`, or `6`
- if the sum mod `3` equals `1`, then the fifth digit can be `2`, `5`, or `8`
- if the sum mod `3` equals `2`, then the fifth digit can be `1`, `4`, or `7`
There are `3` choices for the fifth digit
`color(red)(30000-(8*9*9*9*3))`
3.8: How many ways are there to list the digits `{1,2,2,3,4,5,6}` so that identical digits are not in consecutive positions?
Count the number of ways to list the digits where they are in consecutive positions and subtract from the total number of ways to list the digits
Total number of ways to list digits: `(7!)/(2!)`
Consecutive positions: combine the `2`'s into one `2`, then there are `6!` ways to list the digits
`color(red)((7!)/(2!) - 6!)`
Alternatively, there are `6` positions where the `2`'s could go, then there are `5!` ways to rearrange the remaining digits `implies 6*5! = 6!`
3.9: How many ways are there to list the digits `{1,1,2,2,3,4,5}` so that the two `1`'s are in consecutive positions?
Combine the two `1`'s together into one `1`, then there are `(6!)/(2!)` ways to list the digits
`color(red)((6!)/(2!))`
Alternatively, there are `6` positions where the `1`'s could go, then there are `(5!)/(2!)` ways to rearrange the remaining digits `implies 6*(5!)/(2!) = (6!)/(2!)`
3.10: A cashier wants to work five days a week, but he wants to have at least one of Saturday and Sunday off. In how many ways can he choose the days he will work?
Count the number of ways where he works on Saturday and Sunday and subtract from the total number of ways to choose the five days
Total number of ways to choose five days: `((7),(5))`
Works on Saturday and Sunday: `((5),(3))`
`color(red)(((7),(5))-((5),(3)))`
3.11: A car dealership employs five salespeople. Yesterday the dealership sold seven cars. In how many different ways could this happen?
This is a `7`-element multiset of `[5]`
Alternatively, it is also a weak composition of `7` into `5` parts
`color(red)(((11),(7)))`
3.12: A traveling agent has to visit four cities, each of them five times. In how many different ways can he do this if he is not allowed to start and finish in the same city?
Count the number of ways to do this where he starts and finishes in the same city and subtract from the total number of ways to visit four cities five times each
Consider a random permutation of cities
Total number of ways:
- There are `20!` ways to rearrange them
- But there are `4` sets of `5` duplicate cities
- `implies (20!)/(5!5!5!5!)`
Start and finish in the same city:
- Choose `1` city that will be the start and finish
- There are `18!` ways to rearrange the cities
- But there are `3` sets of `5` duplicate cities and `1` set of `3` duplicate cities
- There are `4` choices for the cities that are fixed at the start and end
- `implies 4*(18!)/(5!5!5!3!)`
`color(red)((20!)/(5!5!5!5!) - 4*(18!)/(5!5!5!3!))`
3.14: A restaurant offers five soups, ten main courses, and six desserts. Joe decided to order at most one soup, at most one main course, and at most one dessert. In how many ways can he do this?
For each meal, not getting it is an option
There are `6` choices for soup
There are `11` choices for soup
There are `7` choices for soup
`color(red)(6*11*7)`
3.18: How many `6`-digit positive integers are there in which the sum of the digits is at most `51`?
Count the number of `6`-digit positive integers in which the sum of the digits is more than `51` and subtract from the total number of `6`-digit positive integers
Total number of `6`-digit positive integers: `999999-100000+1 = 900000`
There are `4` situations where the sum of the digits is more than `51`:
- six `9`'s: `1` way to do this
- five `9`'s and one `8`: `6` ways to do this
- five `9`'s and one `7`: `6` ways to do this
- four `9`'s and two `8`'s: `((6),(2))` ways to do this
`color(red)(900000-(1+6+6+((6),(2))))`
3.19: How many ways are there to select an `11`-member soccer team and a `5`-member basketball team from a class of `30` students if
(a) nobody can be on `2` teams
(b) any number of students can be on both teams
(c) at most one student can be on both teams?
(a) First, pick `11` students for the soccer team: `((30),(11))`
From the remaining `19` students, pick `5` of them to be on the basketball team: `((19),(5))`
`color(red)(((30),(11))*((19),(5)))`
(b) First, pick `11` students for the soccer team: `((30),(11))`
Since we can have students on both teams, we can pick `5` students for the basketball team from the same set of `30` students: `((30),(5))`
`color(red)(((30),(11))*((30),(5)))`
(c) It is valid to have a situation where no student is on both teams. This is part (a): `((30),(11))*((19),(5))`
The (only) other valid situation is to have `1` student on both teams
First, pick `10` students for the soccer team: `((30),(10))`
(the `11^(th)` spot is reserved for the student who is on both teams)
From the remaining `20` students, pick `4` of them to be on the basketball team: `((20),(4))`
(the `4^(th)` spot is reserved for the student who is on both teams)
From the remaining `16` students, pick `1` of them to be on both teams: `16`
`color(red)(((30),(11))*((19),(5)) + ((30),(10))*((20),(4))*16)`
Alternatively, first pick the student who will be on both teams: `30`
From the remaining `29` students, pick `10` of them to be on the soccer team: `((29),(10))`
From the remaining `19` students, pick `4` of them to be on the basketball team: `((19),(4))`
`color(red)(((30),(11))*((19),(5)) + 30*((29),(10))*((19),(4)))`
3.20: Suppose all cars have license plates consisting of six numerical digits only. How many license plates have only one digit that occurs more than once and that digit occurs exactly three times? For example, `404824`.
Pick the digit that will occur three times: `10` choices
From the six positions, pick three of them to be the places where the repeated digit will be: `((6),(3))`
The rest of the digits have to be distinct since there is only one digit that occurs more than once
The fourth digit, regardless of position, has `9` choices
The fifth digit, regardless of position, has `8` choices
The sixth digit, regardless of position, has `7` choices
`color(red)(10*((6),(3))*9*8*7)`
Alternatively,
There are `10` choices for the digit that appears three times
There are `9` choices for the fourth digit
There are `8` choices for the fifth digit
There are `7` choices for the sixth digit
There are `(6!)/(3!)` ways to arrange the six digits
`color(red)(10*9*8*7*(6!)/(3!))`
3.23: In how many different ways can we place `8` identical rooks on a chess board so that no two of them attack each other?
Place a rook on any row/column: `8` choices
There are `7` remaining rows/columns for the next rook
There are `6` remaining rows/columns for the next rook
`vdots`
There is `1` remaining row/column for the last rook
`color(red)(8!)`
Alternatively, place the `8` rooks in such a way so that none of them are attacking each other (e.g. place them all along a diagonal)
There are `8!` ways to rearrange them and still have them not attacking each other
(swapping two rows/columns will ensure that they are still not attacking each other)
3.25: How many three-digit positive integers contain two (but not three) different digits?
Count the number of three-digit positive integers that contain only one different digit and the number of three-digit positive integers that contain three different digits and subtract both from the total number of three-digit positive integers
Total number of three-digit positive integers: `999-100+1 = 900`
three-digit positive integers with only one different digit:
- one different digit means all three digits are the same and there are `9` of these
three-digit positive integers with three different digits:
- There are `9` choices for the first digit (can't be `0`)
- There are `9` choices for the second digit (can't be the first digit but can be `0`)
- There are `8` choices for the third digit
`color(red)(900-9-9*9*8)`
3.27: How many subsets does `[n]` have that contain exactly one of the elements `1` and `2`?
Consider the subsets of `{3,4,...,n}`
There are `n-2` elements `implies 2^(n-2)` subsets
For each subset, there are `2` choices: put a `1` or put a `2`
`2*2^(n-2) = color(red)(2^(n-1))`
3.28: How many subsets does `[n]` have that contain at least one of the elements `1` and `2`?
Consider the subsets of `{3,4,...,n}`
There are `n-2` elements `implies 2^(n-2)` subsets
For each subset, there are `3` choices: put a `1`, put a `2`, or put both
`color(red)(3*2^(n-2))`
3.29: How many three-digit positive integers start and end with an even digit?
There are `4` choices for the first digit (can't be `0`)
There are `10` choices for the second digit
There are `5` choices for the third digit
`color(red)(4*10*5)`
3.30: How many four-digit positive integers are there in which all digits are different?
There are `9` choices for the first digit (can't be `0`)
There are `9` choices for the second digit
There are `8` choices for the third digit
There are `7` choices for the fourth digit
`color(red)(9*9*8*7)`
3.31: How many four-digit positive integers are there that contain the digit `1`?
Count the number of four-digit positive integers that don't contain the digit `1` and subtract from the total number of four-digit positive integers
Total number of four-digit positive integers: `9999-1000+1 = 9000`
Don't contain `1`:
- There are `8` choices for the first digit (can't be `0` or `1`)
- There are `9` choices for the second digit (can't be `1`)
- There are `9` choices for the third digit (can't be `1`)
- There are `9` choices for the fourth digit (can't be `1`)
`color(red)(9000-8*9*9*9)`
3.32: How many three-digit numbers are there in which the sum of the digits is even?
There are four situations where the sum of the digits is even:
- All digits are even
- even odd odd
- odd even odd
- odd odd even
For the case where all digits are even:
- There are `4` choices for the first digit (can't be `0`)
- There are `5` choices for the second digit
- There are `5` choices for the third digit
- `implies 4*5*5 = 100`
For even odd odd:
- There are `4` choices for the first digit (can't be `0`)
- There are `5` choices for the second digit
- There are `5` choices for the third digit
- `implies 4*5*5 = 100`
For odd even odd:
- There are `5` choices for the first digit (can't be `0`)
- There are `5` choices for the second digit
- There are `5` choices for the third digit
- `implies 5*5*5 = 125`
For odd odd even:
- There are `5` choices for the first digit (can't be `0`)
- There are `5` choices for the second digit
- There are `5` choices for the third digit
- `implies 5*5*5 = 125`
`color(red)(100+100+125+125 = 450)`
3.33: In how many ways can the elements of `[n]` be permuted if
(a) `1` is to precede `2` and `3` is to precede `4`
(b) `1` is to precede both `2` and `3`?
(a) Consider the set `[4]`
There are six situations where this happens:
- `1234`
- `1324`
- `1342`
- `3214`
- `3124`
- `3142`
Now consider adding `5`
There are `5` choices where it could be placed for each of the six situations
Now consider adding `6`
There are `6` choices where it could be placed for each of the six situations
`vdots`
Now consider adding `n`
There are `n` choices where it could be placed for each of the six situations
`color(red)(6*(n)_(n-4) = 6*n*(n-1)*...*6*5)`
(b) Consider the set `[3]`
There are two situations where this happens:
- `123`
- `132`
Now consider adding `4`
There are `4` choices where it could be placed for each of the two situations
`vdots`
Now consider adding `n`
There are `n` choices where it could be placed for each of the two situations
`color(red)(2*(n)_(n-2) = 2*n*(n-1)*...*5*4)`
3.37: A student needs to work five days in January. He does not want to work on more than one Sunday. In how many ways can he select his five working days? (Assume that January has five Sundays.)
There are two situations:
- none of the days is Sunday
- one of the days is Sunday
For the case where none of the days is Sunday, there are `26` days to choose from: `((26),(5))`
For the case where one of the days is Sunday:
- Pick `4` days that aren't Sunday: `((26),(4))`
- There are `5` positions for the Sunday (e.g. Sunday can be the first day, second day, ..., fifth day)
- `implies 5*((26),(4))`
`color(red)(((26),(5))+5*((26),(4)))`
3.38: A host invites `n` couples to a party. She wants to ask a subset of the `2n` guests to give a speech, but she does not want to ask both members of any couple to give speeches. In how many ways can she proceed?
For each of the `n` couples there are `3` options:
- no person speaks
- partner `1` speaks
- partner `2` speaks
`color(red)(3^n)`
3.40: How many different ways can we select ordered pairs `(A,B)` of subsets of `[n]` so that `A nn B != O/`?
Count the number of ways to pick ordered pairs `(A,B)` such that `A nn B = O/` and subtract from the total number of ways to select ordered pairs `(A,B)`
Total number of ways to pick ordered pairs `(A,B)`:
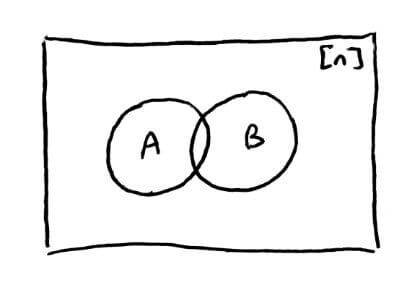
Any element in `[n]` can be:
- `in A` and `in B`
- `in A` and `notin B`
- `notin A` and `in B`
- `notin A` and `notin B`
`4^n` ways
For the case where `A nn B = O/`:
Any element can be:
- `in A and notin B`
- `notin A and in B`
- `notin A and notin B`
`3^n` ways
`color(red)(4^n-3^n)`
3.41: How many different ways are there to select three subsets `A`,`B`, and `C` of `[n]` so that `A sube C`, `B sube C` and `A nn B != O/`?
Count the number of way to pick subsets so that `A nn B = O/` and subtract from the total number of ways to pick subsets
Total number of ways to pick subsets:
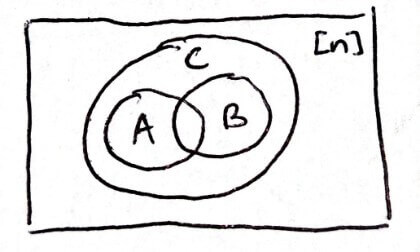
Any element in `[n]` can be:
- `in A and in B`
- `in A and notin B`
- `notin A and in B`
- `notin A and notin B and in C`
- `notin A and notin B and notin C`
`5^n` ways
For the case where `A nn B = O/`:
Any element in `[n]` can be:
- `in A and notin B`
- `notin A and in B`
- `notin A and notin B and in C`
- `notin A and notin B and notin C`
`4^n` ways
`color(red)(5^n-4^n)`
3.42: A two-day math conference has `n` participants. Some of the participants give a talk on Saturday, some others give a talk on Sunday. Nobody gives more than one talk, and there may be some people who do not give a talk at all. At the end of the conference, a few talks are selected to be included in a book. In how many different ways is this all possible if there is at least one talk selected for inclusion in the book?
Count the number of ways for people to give talks without any of them being included in the book and subtract from the total number of ways for people to give talks
Total number of ways for people to give talks:
There are five situations for each person:
- don't give a talk at all
- give a talk on Saturday
- give a talk on Sunday
- be included in the book as a Saturday speaker
- be included in the book as a Sunday speaker
`5^n` ways
For the case where no talk is selected to be in the book, there are three situations for each person:
- don't give a talk at all
- give a talk on Saturday
- give a talk on Sunday
`3^n` ways
`color(red)(5^n-3^n)`
3.43: A group organizing a faculty-student tennis match must match four faculty volunteers to four of the `13` students who volunteered to be in the match. In how many ways can they do this?
The first faculty volunteer has `13` students from which to choose
The second faculty volunteer has `12` students from which to choose
The third faculty volunteer has `11` students from which to choose
The fourth faculty volunteer has `10` students from which to choose
`color(red)(13*12*11*10)`
3.45: A student will study `26` hours in preparation for an exam. She will do this in the course of six consecutive days. On each of these days, she will study either four hours, five hours, or six hours. In how many different ways is this possible?
Let `a` be the number of days she studies for four hours
Let `b` be the number of days she studies for five hours
Let `c` be the number of days she studies for six hours
Considering the conditions, we get the system of equations
`a+b+c = 6`
`4a+5b+6c = 26`
`implies b + 2c = 2`
So `b = 2, c = 0, a = 4` (five hours for `2` days and four hours for `4` days)
or
`b = 0, c = 1, a = 5` (six hours for `1` day and four hours for `5` days)
For the case where she studies for four hours for `4` days and five hours for `2` days:
- There are `6` days to choose from and `4` of them could be for the four hours
- `((6),(4)) = 15`
- Alternatively, there are `6` days to choose from and `2` of them could be for the five hours
- `((6),(2)) = 15`
For the case where she studies for four hours for `5` days and six hours for `1` day:
- There are `6` days to choose from and `5` of them could be for the four hours
- `((6),(5)) = 6`
- Alternatively, there are `6` days to choose from and `1` of them could be for the six hours
- `((6),(1)) = 6`
`color(red)(15+6 = 21)`
3.46: Andy and Brenda throw four dice at the same time. If at least one of the four dice shows a six, then Andy wins, if not then Brenda. Who has a greater chance of winning?
Calculate Brenda's chance of winning by counting the number of possibilities where none of the dice show a six
Total number of possibilities:
- Each die has `6` possible outcomes `implies 6^4`
None of them show a six:
- Each die has `5` possible outcomes `implies 5^4`
Brenda has a `(5^4)/(6^4) = 625/1296` chance of winning
Andy has a `671/1296` chance of winning
`color(red)(text(Andy))`
3.49: A class is attended by `n` sophomores, `n` juniors, and `n` seniors. In how many ways can these students form `n` groups of three people each if each group is to contain a sophomore, a junior, and a senior?
For the first sophomore, there are `n` choices of juniors and `n` choices of seniors
For the second sophomore, there are `n-1` choices of juniors and `n-1` choices of seniors
For the third sophomore, there are `n-2` choices of juniors and `n-2` choices of seniors
`vdots`
For the last sophomore, there is `1` choice for the junior and `1` choice for the senior
`color(red)(n!*n!)`
3.50: The NFL consists of `32` teams. These teams are first divided into two conferences, the American Conference and the National Conference, each of which consists of sixteen teams. Then each conference is divided into four divisions of four teams each. Each division has a distinct name. In how many ways can this be done?
There are a total of `8` divisions
There are `((32),(4))` choices for the first division
There are `((28),(4))` choices for the second division
There are `((24),(4))` choices for the third division
`vdots`
There are `((8),(4))` choices for the seventh division
There are `((4),(4))` choices for the eighth division
`color(red)(((32),(4))*((28),(4))*((24),(4))*...*((8),(4))*((4),(4)))`
Chapter 5
5.19: What is the number of partitions of `[8]` into two blocks in which the two blocks do not have the same size?
There are `3` situations where the two blocks do not have the same size:
- size `1` and size `7`: `((8),(1)) = ((8),(7))` ways to do this
- size `2` and size `6`: `((8),(2)) = ((8),(6))` ways to do this
- size `3` and size `5`: `((8),(3)) = ((8),(5))` ways to to this
`color(red)(((8),(1))+((8),(2))+((8),(3)))`
5.20: What is the number of compositions of `5` with a unique largest part?
There are five types of compositions of `5` with a unique largest part:
- `(1,1,1,2)`: `4` permutations
- `(1,1,3)`: `3` permutations
- `(1,4)`: `2` permutations
- `(2,3)`: `2` permutations
- `(5)`: `1` permutation
`color(red)(1+2+2+3+4 = 12)`
5.22: A student has to take twelve hours of classes a week. She must take at least three hours on Monday, at least two on Thursday, and at least one on Friday. In how many ways can she do this?
Let `a,b,c,d,e` be the number of hours she takes on Monday, Tuesday, Wednesday, Thursday, and Friday respectively
`a+3 + b + c + d+2 + e+1 = 12`
`a+b+c+d+e = 6`
This is a weak composition of `6` into `5` parts
`color(red)(((10),(6)))`
5.23: Find the number of compositions of ten into even parts
`2x_1 + 2x_2 + ... + 2x_n = 10`
`2(x_1 + x_2 + ... + x_n) = 10`
`x_1 + x_2 + ... + x_n = 5`
This is the same problem as the number of compositions of `5` into integer parts
`color(red)(2^(5-1) = 2^4 = 16)`
5.24: Find the number of weak compositions of `25` into five odd parts
`x_1 + x_2 + x_3 + x_4 + x_5 = 25` where `x_1, ..., x_5` are odd integers
Let `x_i = 2y_i+1`
`2y_1+1 + 2y_2+1 + 2y_3+1 + 2y_4+1 + 2y_5+1 = 25`
`2(y_1 + y_2 + y_3 + y_4 + y_5) = 20`
`y_1 + y_2 + y_3 + y_4 + y_5 = 10`
This is a weak composition of `10` into `5` parts
`color(red)(((14),(10)))`
5.25: A student has to take eight hours of classes a week. He wants to have fewer hours on Friday than on Thursday. In how many ways can he do this?
Let `a,b,c,d,e` be the number of hours he takes on Monday, Tuesday, Wednesday, Thursday, and Friday respectively
`a+b+c+d+e = 8` where `d gt e`
He could take `0, 1, 2, 3` hours on Friday
Since he wants fewer hours on Friday than on Thursday, we add `e+1` hours to `d` to maintain the rule `d gt e` and to turn the problem into a weak composition problem
`e=0: a+b+c+(d+1)+0=8 implies a+b+c+d=7 implies ((10),(7))`
`e=1: a+b+c+(d+2)+1=8 implies a+b+c+d=5 implies ((8),(5))`
`e=2: a+b+c+(d+3)+2=8 implies a+b+c+d=3 implies ((6),(3))`
`e=3: a+b+c+(d+4)+3=8 implies a+b+c+d=1 implies ((4),(1))`
`color(red)(((10),(7))+((8),(5))+((6),(3))+((4),(1)))`
5.27: Find a closed formula for `S(n,n-2)` for all `n ge 3`
There are only two ways to have `n-2` blocks:
- one block of size `3` and `n-3` singletons: `((n),(3))`
- two blocks of size `2` and `n-4` singletons: `((n),(4))*((4),(2))*1/2` (choose four numbers to be in the two blocks, then choose two of those four numbers to be in one of the blocks, the order of the blocks don't matter)
`color(red)(((n),(3))+((n),(4))*((4),(2))*1/2)`
Alternatively, for the two blocks of size `2`, we could choose two numbers to be in one block, then choose another two to be in the other block: `((n),(2))*((n-2),(2))*1/2`
5.28: Find a closed formula for `S(n,n-3)` for all `n ge 4`
There are only `3` ways to have `n-3` blocks:
- one block of size `4` and `n-4` singletons: `((n),(4))`
- one block of size `3`, one block of size `2` and `n-5` singletons: `((n),(5))*((5),(3))` (choose `5` to be in the two blocks, then choose `3` to be in the block of size `3`)
- three blocks of size `2` and `n-6` singletons: `((n),(2))*((n-2),(2))*((n-4),(2))*1/(3!)`
`color(red)(((n),(4))+((n),(5))*((5),(3))+((n),(2))*((n-2),(2))*((n-4),(2))*1/(3!))`
Alternatively, for the one block of size `3`, we could do `((n),(3))*((n-3),(2))`
5.32: Let `F(n)` be the number of all partitions of `[n]` with no singleton blocks. Prove that `B(n) = F(n) + F(n+1)`
`B(n)-F(n)` is the number of partitions of `[n]` where each partition has at least one singleton
Goal: Prove `B(n)-F(n) = F(n+1)`
Claim: There is a bijection between `A = {`partitions of `[n]` such that there is at least one singleton`}` and `B = {`partitions of `[n+1]` such that every block has size `gt 1}`
Let `f:A rarr B` be defined as follows:
For a partition in `A`, add the singleton `{n+1}` and merge together all the singleton blocks into one block
This produces an element in `B` because there are no singleton blocks, i.e., every block has size `gt 1`
Let `g:B rarr A` be defined as follows:
For a partition in `B`, break up the block containing `n+1` into singletons and remove the singleton `{n+1}`
This produces an element in `A` because there are now singleton blocks, i.e., there is at least one block with size `1`
So `g` is the inverse of `f`
`implies f` is a bijection
`implies |A| = |B|`
`implies B(n)-F(n) = F(n+1)`
`implies B(n) = F(n) + F(n+1)`
Chapter 4
4.3: Prove that `2^(n-2)*n*(n-1) = sum_(k=2)^n k(k-1)((n),(k))` for all integers `n ge 2`
Start with the binomial theorem
`(x+y)^n = sum_(k=2)^n((n),(k))x^ky^(n-k)`
Take the derivative (with respect to `x`) of both sides twice
`n*(x+y)^(n-1) = sum_(k=2)^n((n),(k))kx^(k-1)y^(n-k)`
`n*(n-1)*(x+y)^(n-2) = sum_(k=2)^n((n),(k))k(k-1)x^(k-2)y^(n-k)`
Plug in `x=y=1`
`n*(n-1)*2^(n-2) = sum_(k=2)^n((n),(k))k(k-1)`
4.4: Let `k,m,n` be nonnegative integers integers such that `k+m le n`. Prove that `((n),(m))*((n-m),(k)) = ((n),(k))((n-k),(m))`
The left-hand side is counting the number of ways to
- Pick `m` people to form a soccer team from a group of `n` people
- Then pick `k` people from the remaining people (`n-m`) to form a basketball team
The right-hand side is counting the number of ways to
- Pick `k` people to form a basketball team from a group of `n` people
- Then pick `m` people from the remaining people (`n-k`) to form a soccer team
Both are counting the number of ways to form an `m`-member soccer team and a `k`-member basketball team
4.8: Prove that for all positive integers `n`, the inequality `((2n),(n)) lt 4^n` holds
`((2n),(n))` is the number of `n`-element subsets of `[2n]`
`4^n = 2^(2n)` is the number of all subsets of `[2n]`
4.9: How many subsets of `[n]` are larger than their complements?
Pair each subset with its complement
If `n` is odd:
- The two subsets in each pair will be different sizes, so there will be a larger subset in each pair
- There are `2^(n-1)` unique pairs, so there are `color(red)(2^(n-1))` subsets larger than their complement
If `n` is even, then let `n = 2k`
`sum_(i=0)^(k-1)((n),(i))` counts the number of subsets that are larger than their complements
To get that summation, we could split the subsets of `[n]` into three groups:
- Subsets with size `0 le i le k-1`: `sum_(i=0)^(k-1)((n),(i))=((n),(1))+((n),(2))+...+((n),(k-1))`
- Subsets with size `k=n/2`: `((n),(k))=((n),(n/2))`
- Subsets with size `k+1 le i le n`: this is the "reverse" of `0 le i le k-1`, so it is also counted by `sum_(i=0)^(k-1)((n),(i))`
So we have
`2^n = ((n),(n/2))+2sum_(i=0)^(k-1)((n),(i))`
`2sum_(i=0)^(k-1)((n),(i)) = 2^n-((n),(n/2))`
`sum_(i=0)^(k-1)((n),(i)) = (2^n-((n),(n/2)))/2`
`sum_(i=0)^(k-1)((n),(i)) = color(red)(2^(n-1)-1/2((n),(n/2)))`
4.17: Prove that `sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))=3^n`
Start with the multinomial theorem
`sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))x_1^(a_1)x_2^(a_2)x_3^(a_3) = (x_1+x_2+x_3)^n`
Plug in `x_1=x_2=x_3=1`
`sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))=3^n`
4.18: Prove that `sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))(-1)^(a_2)=1`
Start with the multinomial theorem
`sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))x_1^(a_1)x_2^(a_2)x_3^(a_3) = (x_1+x_2+x_3)^n`
Plug in `x_1=x_3=1`, `x_2=-1`
`sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))(-1)^n=(1-1+1)^n`
`sum_(a_1+a_2+a_3=n)((n),((a_1,a_2,a_3)))(-1)^n=1`
4.25: Find a closed form for `sum_(n=1)^(oo)nx^(n-1)`
Since there's an `n` dropped down from the exponent, it looks like we have to take the derivative of `sum_(n=0)^(oo)x^n = 1/(1-x)`
Take out the constant term from `sum_(n=0)^(oo)x^n` in order to take the derivative
`sum_(n=0)^(oo)x^n=1+sum_(n=1)^(oo)x^n = 1/(1-x)`
Taking the derivative, we get
`sum_(n=1)^(oo)nx^(n-1) = color(red)(1/(1-x)^2)`
4.26: Prove that `1/sqrt(1-4x) = sum_(n ge 0)((2n),(n))x^n`
`1/sqrt(1-4x) = (1-4x)^(-1/2)`
`= sum_(n ge 0)((-1/2),(n))(-4x)^n`
`= sum_(n ge 0)((-1/2)(-3/2)(-5/2)...(-2n+1)/2)/(n!)(-1)^n2^(2n)x^n`
`= sum_(n ge 0)(1*3*5*...*(2n-1))/(n!)2^nx^n`
Now we have to show that `((2n),(n)) = ((2n)!)/(n!n!) = (1*3*5*...*(2n-1))/(n!)2^n`, which is the same as showing `((2n)!)/(n!) = 1*3*5*...*(2n-1)*2^n`
For `((2n)!)/(n!)`, all the terms on the bottom will divide all the even terms on top in half, resulting in `2^n` and all the odd terms leftover, which is `1*3*5*...*(2n-1)*2^n`
4.35: A school has `105` students and seven classes. If each student takes three classes, and each class is taken by the same number of students, how many students are taking each class?
Count the number of pairs `(x,c)` where `x` is a student and `c` is a class
There are `105*3 = 315` pairs
Distribute the pairs among `7` groups so that each group has the same number of pairs
So there are `color(red)(315/7 = 45)` students in each class
4.36: How many northeastern lattice paths are there from `(0,0)` to `(10,10)` that do not touch the point `(5,5)`, but do touch the point `(3,3)`?
Count the paths from `(0,0)` to `(3,3)`:
`((6),(3))`
(`6` steps total, choose `3` to be right/up)
Count the paths from `(3,3)` to `(10,10)`
`((14),(7))`
Since we can't go through `(5,5)`, count the number of paths going through `(5,5)` and subtract from the total number of paths
Paths from `(3,3)` to `(5,5)`:
`((4),(2))`
Paths from `(5,5)` to `(10,10)`
`((10),(5))`
Paths from `(3,3)` to `(10,10)` that go through `(5,5)`:
`((4),(2))*((10),(5))`
Paths from `(3,3)` to `(10,10)` that don't go through `(5,5)`:
`((14),(7))-((4),(2))*((10),(5))`
Paths from `(0,0)` to `(10,10)` that don't go through `(5,5)`:
`color(red)(((6),(3))*[((14),(7))-((4),(2))*((10),(5))])`
4.38: Prove that `((2n),(n)) = sum_(k=0)^n((n),(k))^2` for all positive integers `n`
Note that `((n),(k))^2 = ((n),(k))*((n),(k)) = ((n),(k))*((n),(n-k))`
The left-hand side is counting the number of ways to pick `n` people from a group of `2n` people
We could pick people another way by splitting the `2n` people into two groups of `n` people
Pick `k` people from the first group: `((n),(k))`
Now we have to pick `n-k` people from the second group: `((n),(n-k))`
Summing over all `k`, we get the result
`((2n),(n)) = sum_(k=0)^n((n),(k))*((n),(n-k))`
`((2n),(n)) = sum_(k=0)^n((n),(k))*((n),(k))`
`((2n),(n)) = sum_(k=0)^n((n),(k))^2`
4.39: Prove that `n((2n-1),(n-1)) = sum_(k=1)^nk((n),(k))^2` for all positive integers `n`
Note that `((n),(k))^2 = ((n),(k))*((n),(k)) = ((n),(k))*((n),(n-k))`
The left-hand side is counting the number of ways to form a group of `n` people with a leader from a group of `2n` people
First, pick the leader from `n` people, then pick `n-1` people from `2n-1` people to form the group
We could pick people another way by splitting the `2n` people into two groups of `n` people and picking a leader from the first group
Pick `k` people from the first group: `((n),(k))`
Pick a leader from the first group: there are `k` choices
Now we have to pick `n-k` people from the second group: `((n),(n-k))`
Summing over all `k`, we get the result
`n((2n-1),(n-1)) = sum_(k=1)^nk((n),(k))*((n),(n-k))`
`n((2n-1),(n-1)) = sum_(k=1)^nk((n),(k))*((n),(k))`
`n((2n-1),(n-1)) = sum_(k=1)^nk((n),(k))^2`
4.40: Prove that `3^n = sum_(k=0)^n2^k((n),(k))` for all positive integers `n`
Start with the binomial theorem:
`(x+y)^n = sum_(k=0)^n((n),(k))x^ky^(n-k)`
Plug in `x=2, y=1`:
`(2+1)^n = sum_(k=0)^n((n),(k))2^k1^(n-k)`
`3^n = sum_(k=0)^n((n),(k))2^k`
4.45: Prove that `sum_(k=0)^n((n),(k))2^k = (3^n+(-1)^n)/2` for all positive integers `n` and even `k`
(Refer to the trick for getting rid of even/odd terms of a formal power series in the egf section)
We can isolate the even terms by adding `sum_(k=0)^n((n),(k))(-2)^k` to `sum_(k=0)^n((n),(k))2^k`
`sum_(k=0)^n((n),(k))2^k = ((n),(0))2^0 + ((n),(1))2^1 + ((n),(2))2^2 + ((n),(3))2^3 + ...`
`sum_(k=0)^n((n),(k))(-2)^k = ((n),(0))(-2)^0 + ((n),(1))(-2)^1 + ((n),(2))(-2)^2 + ((n),(3))(-2)^3 + ...`
Notice that the terms with odd exponents will cancel out after addition, leaving
`2 + 2((n),(2))2^2 + 2((n),(4))2^4 + ...`
Dividing by `2` will give us
`1 + ((n),(2))2^2 + ((n),(4))2^4 + ...`
`= sum_(k=0)^n((n),(k))2^k` for even `k`
Using the binomial theorem, we can simplify `sum_(k=0)^n((n),(k))2^k` and `sum_(k=0)^n((n),(k))(-2)^k`
`sum_(k=0)^n((n),(k))2^k = (2+1)^n = 3^n`
`sum_(k=0)^n((n),(k))(-2)^k = (-2+1)^n = (-1)^n`
Adding those and dividing the sum by `2` gives us
`(3^n+(-1)^n)/2`
which is equal to `sum_(k=0)^n((n),(k))2^k` for even `k` as shown at the beginning
4.46: Prove that `sum_(k=1)^n((n),(k))5^k = (6^n-(-4)^n)/2` for all positive integers `n` and odd `k`
(Refer to the trick for getting rid of even/odd terms of a formal power series in the egf section)
We can isolate the odd terms by subtracting `sum_(k=0)^n((n),(k))(-5)^k` from `sum_(k=0)^n((n),(k))5^k`
`sum_(k=0)^n((n),(k))5^k = ((n),(0))5^0 + ((n),(1))5^1 + ((n),(2))5^2 + ((n),(3))5^3 + ...`
`sum_(k=0)^n((n),(k))(-5)^k = ((n),(0))(-5)^0 + ((n),(1))(-5)^1 + ((n),(2))(-5)^2 + ((n),(3))(-5)^3 + ...`
Notice that the terms with even exponents will cancel out after subtraction, leaving
`2((n),(1))5^1 + 2((n),(3))5^3 + ...`
Dividing by `2` will give us
`((n),(2))5^1 + ((n),(3))5^3 + ...`
`= sum_(k=1)^n((n),(k))5^k` for odd `k`
Using the binomial theorem, we can simplify `sum_(k=0)^n((n),(k))5^k` and `sum_(k=0)^n((n),(k))(-5)^k`
`sum_(k=0)^n((n),(k))5^k = (5+1)^n = 6^n`
`sum_(k=0)^n((n),(k))(-5)^k = (-5+1)^n = (-4)^n`
Adding those and dividing the sum by `2` gives us
`(6^n+(-4)^n)/2`
which is equal to `sum_(k=0)^n((n),(k))5^k` for odd `k` as shown at the beginning
4.49: What is the coefficient of `x^n` in the power series form of `root(3)(1-2x)`?
`root(3)(1-2x) = (1-2x)^(1/3)`
Start with the general binomial theorem:
`(1+x)^m = sum_(n ge 0)((m),(n))x^n`
Plug in `x=-2x` and `m=1/3`
`(1-2x)^(1/3) = sum_(n ge 0)((1/3),(n))(-2x)^n`
`(1-2x)^(1/3) = sum_(n ge 0)((1/3),(n))(-2)^nx^n`
So the coefficient of `x^n` is `color(red)(((1/3),(n))(-2)^n)`
Chapter 8
8.1: Find an explicit formula for `a_k` if `a_0=0` and `a_(k+1)=a_k+2^k` for `k ge 0`
`a_1 = a_0 + 2^0 = 2^0`
`a_2 = a_1 + 2^1 = 2^0+2^1`
`a_3 = a_2 + 2^2 = 2^0+2^1+2^2`
`vdots`
`a_k = 2^0+2^1+2^2+...+2^(k-1) = sum_(i=0)^(k-1)2^i`
We can think of `sum_(i=0)^(k-1)2^i` as a binary digit with `k` `1`'s
`ubrace(111...111)_k`
Adding `1` to that binary digit results in a `1` followed by `k` `0`'s, which is `2^k`
`1ubrace(000...000)_k`
So `a_k = sum_(i=0)^(k-1)2^i = color(red)(2^k-1)`
8.4: A child wants to walk up a stairway. At each step, she moves up either one or two stairs. Let `f(n)` be the number of ways she can reach the `n^(th)` stair. Let `F(x) = sum_(n ge 0)f_nx^n` be the generating function. Express `F(x)` as a rational function
She can reach the `n^(th)` step from either the `(n-1)^(st)` step or the `(n-2)^(nd)` step
So `f(n) = f(n-1) + f(n-2) implies f(n+2) = f(n+1) + f(n)`
Let `f(0)=1`
Multiply the recurrence by `x^(n+2)` and sum over all `n ge 0`
`sum_(n ge 0)f(n+2)x^(n+2) = sum_(n ge 0)f(n+1)x^(n+2) + sum_(n ge 0)f(n)x^(n+2)`
`F(x)-f(0)-f(1)x = xsum_(n ge 0)f(n+1)x^(n+1) + x^2sum_(n ge 0)f(n)x^n`
`F(x)-1-x = x(F(x)-f(0)) + x^2F(x)`
`F(x)-1-x = xF(x)-x+x^2F(x)`
`F(x)-xF(x)-x^2F(x)=1`
`F(x)(1-x-x^2)=1`
`color(red)(F(x)=1/(1-x-x^2))`
8.7: Let `a_n` be the number of ways to pay `n` dollars using ten-dollar bills, five-dollar bills, and one-dollar bills only. Find the ordinary generating function `A(x) = sum_(n ge 0)a_nx^n`
Let `B(x)` be the generating function for the number of ways to pay `n` dollars using only ten-dollar bills
Let `C(x)` be the generating function for the number of ways to pay `n` dollars using only five-dollar bills
Let `D(x)` be the generating function for the number of ways to pay `n` dollars using only one-dollar bills
Then the product `B(x)C(x)D(x)` will be the number of ways to pay `n` dollars using those three types of bills
For `B(x)`, there are no ways to pay `n` dollars using only ten-dollar bills for `1 le n le 9`, `11 le n le 19`, ..., so
`B(x) = 1+0x+0x^2+...+1x^10+0x^11+...+1x^20+...=1+x^10+x^20+...=1/(1-x^10)`
Similarly for `C(x)` and `D(x)`
`C(x) = 1+x^5+x^10+...=1/(1-x^5)`
`D(x) = 1+x^1+x^2+...=1/(1-x)`
So `A(x)=B(x)C(x)D(x)=color(red)(1/((1-x^10)(1-x^5)(1-x)))`
8.8: Find a simple, closed form for the generating function of the sequence defined by `a_n=n^2`. Hint: `n^2 = 2((n),(2))+n`
Multiply the recurrence by `x^n` and sum over all `n`:
`sum_(n ge 0)a_nx^n = sum_(n ge 0)2((n),(2))x^n + sum_(n ge 0)nx^n`
Simplifying `((n),(2)) = (n*(n-1)*(n-2)!)/(2*(n-2)!) = (n(n-1))/2`, we get
`A(x) = sum_(n ge 2)n(n-1)x^n + sum_(n ge 1)nx^n`
`sum_(n ge 2)n(n-1)x^n` looks like a double derivative and `sum_(n ge 1)nx^n` looks like a derivative
`A(x) = sum_(n ge 0)a_nx^n = 1/(1-x)`
`A'(x) = sum_(n ge 1)na_nx^(n-1) = 1/(1-x)^2`
`A''(x) = sum_(n ge 2)a_n(n-1)x^(n-2) = 2/(1-x)^3`
Taking the derivatives and multiplying by `x` and `x^2` gives us
`A(x) = (2x^2)/(1-x)^3 + x/(1-x)^2`
`= color(red)((x(x+1))/(1-x)^3)`
8.9: Let `f(n)` be the number of subsets of `[n]` in which the distance of any two elements is at least three. Find the generating function of `f(n)`
Consider a subset that satisfies the condition
If `n` is part of the subset, then `n-1` and `n-2` cannot be in the subset
So there would be `f(n-3)` ways to make this subset
If `n` is not part of the subset, then there would be `f(n-1)` ways to make this subset
So we get the recurrence `f(n) = f(n-3)+f(n-1)` for `n ge 3`
`f(0) = 1` (just the empty set)
`f(1) = 2` (the empty set and `{1}`)
`f(2) = 3` (the empty set, `{1}` and `{2}`)
Multiply the recurrence by `x^n` and sum over all `n ge 3`
`sum_(n ge 3)f(n)x^n = sum_(n ge 3)f(n-3)x^n + sum_(n ge 3)f(n-1)x^n`
`F(x)-f(0)-f(1)x-f(2)x^2 = x^3sum_(n ge 3)f(n-3)x^(n-3) + xsum_(n ge 3)f(n-1)x^(n-1)`
`F(x)-1-2x-3x^2 = x^3F(x) + x(F(x)-f(0)-f(1)x)`
`F(x)-1-2x-3x^2 = x^3F(x) + xF(x)-x-2x^2`
`F(x)-x^3F(x)-xF(x) = 1+x+x^2`
`F(x)(1-x-x^3) = 1+x+x^2`
`F(x) = (1+x+x^2)/(1-x-x^3)`
8.22: Let `b(n)` be the number of compositions of `n` in which each part is an odd integer. Find a closed formula for `sum_(n ge 0)b(n)x^n`
Since the number of parts is unspecified, this problem involves a composition of generating functions
This is equivalent to splitting up `[n]` into intervals and covering each interval with a single tile of odd length
If the length of the interval is even, then there is no way to do this
If the length of the interval is odd, then there is one way to do this
`a_n = {(1 text( if n odd)),(0 text( if n even)):}`
So `A(x)=x+x^3+x^5+... = x(1+x^2+x^4+...) = x/(1-x^2)`
So `B(x) = 1/(1-A(x))`
`= 1/(1-x/(1-x^2))`
`= color(red)((1-x^2)/(1-x^2-x))`
8.23: Find an explicit formula for `a_n` if `a_0=1` and `a_(n+1)=3a_n+2^n` if `n ge 0`
Multiply the recurrence by `x^(n+1)` and sum over all `n ge 0`:
`sum_(n ge 0)a_(n+1)x^(n+1) = sum_(n ge 0)3a_nx^(n+1) + sum_(n ge 0)2^nx^(n+1)`
`A(x)-a_0 = 3xsum_(n ge 0)a_nx^n + xsum_(n ge 0)(2x)^n`
`A(x)-1 = 3xA(x)+x/(1-2x)`
`A(x)-3xA(x) = x/(1-2x)+1`
`A(x)(1-3x) = (1-x)/(1-2x)`
`A(x) = (1-x)/((1-2x)(1-3x))`
Using partial fractions, we get
`(1-x)/((1-2x)(1-3x)) = alpha/(1-2x) + beta/(1-3x)`
`1-x = (1-3x)alpha + (1-2x)beta`
`1-x = alpha-3alphax + beta-2betax`
`1-x = (alpha+beta)+(-3alpha-2beta)x`
`implies alpha=-1, beta=2`
`implies (1-x)/((1-2x)(1-3x)) = -1/(1-2x) + 2/(1-3x)`
`= 2sum_(n ge 0)(3x)^n - sum_(n ge 0)(2x)^n`
`= 2sum_(n ge 0)3^nx^n - sum_(n ge 0)2^nx^n`
So `a_n` is the coefficient of `x^n`, which is `color(red)(2*3^n-2^n)`
8.24: Find an explicit formula for `a_n` if `a_0=1,a_1=4` and `a_(n+2)=8a_(n+1)-16a_n` for `n ge 0`
We can use the characteristic polynomial `t^2-c_1t-c_2` where `c_1=8` and `c_2=-16`
`t^2-8t+16=(t-4)(t-4)`
Since the roots are the same there exist `alpha_1,alpha_2` such that `a_n = alpha_1 4^n+alpha_2n4^n`
Plugging in `n=0,1`:
`a_0 = 1 = alpha_1`
`a_1 = 4 = 4alpha_1 + 4alpha_2`
`implies alpha_1 = 1, alpha_2 = 0`
`implies a_n = color(red)(4^n)`
8.25: A certain kind of insect population multiplies so that at the end of each year, its size is the double of its size a year before, plus `1000` more insects. Assuming that originally we released `50` insects, how many of them will we have at the end of the `n^(th)` year?
The recurrence is `a_(n+1) = 2a_n + 1000` for `n ge 0` and `a_0=50`
Multiply the recurrence by `x^(n+1)` and sum over `n ge 0`:
`sum_(n ge 0)a_(n+1)x^(n+1) = sum_(n ge 0)2a_nx^(n+1) + sum_(n ge 0)1000x^(n+1)`
`A(x)-a_0 = 2xsum_(n ge 0)a_nx^n + 1000xsum_(n ge 0)x^n`
`A(x)-50 = 2xA(x) + (1000x)/(1-x)`
`A(x)-2xA(x) = (1000x)/(1-x)+50`
`A(x)(1-2x) = (50+950x)/(1-x)`
`A(x) = (50+950x)/((1-2x)(1-x))`
Using partial fractions, we get:
`(50+950x)/((1-2x)(1-x)) = alpha/(1-2x)+beta/(1-x)`
`50+950x = (1-x)alpha + (1-2x)beta`
`50+950x = alpha-alphax + beta-2betax`
`50+950x = (alpha+beta) + (-alpha-2beta)x`
`implies alpha=1050, beta=-1000`
`implies (50+950x)/((1-2x)(1-x)) = 1050/(1-2x)-1000/(1-x)`
`= 1050sum_(n ge 0)(2x)^n - 1000sum_(n ge 0)x^n`
`= 1050sum_(n ge 0)2^nx^n - 1000sum_(n ge 0)x^n`
So `a_n` is the coefficient of `x^n`, which is `color(red)(1050*2^n-1000)`
8.27: Find an explicit formula for the numbers `a_n` if `a_(n+1) = (n+1)a_n + 2(n+1)!` if `n ge 0` and `a_0 = 0`
Since there's an `(n+1)!`, we should probably use exponential generating functions
Let `A(x) = sum_(n ge 0)a_n/(n!)x^n`
Multiply both sides by `x^(n+1)/((n+1)!)` and sum over `n ge 0`
`sum_(n ge 0)a_(n+1)/((n+1)!)x^(n+1) = sum_(n ge 0)((n+1)a_n)/((n+1)!)x^(n+1) + sum_(n ge 0)(2(n+1)!)/((n+1)!)x^(n+1)`
`A(x)-a_0 = sum_(n ge 0)a_n/(n!)x^(n+1) + sum_(n ge 0)2x^(n+1)`
`A(x) = xsum_(n ge 0)a_n/(n!)x^n + 2xsum_(n ge 0)x^n`
`A(x) = xA(x) = (2x)/(1-x)`
`A(x)-xA(x) = (2x)/(1-x)`
`A(x)(1-x) = (2x)/(1-x)`
`A(x) = (2x)/(1-x)^2`
`A(x) = 2x(1-x)^(-2)`
`A(x) = 2xsum_(n ge 0)((n+1),(n))x^n`
`A(x) = 2sum_(n ge 0)((n+1),(n))x^(n+1)`
`A(x) = 2sum_(n ge 1)((n),(n-1))x^n`
`A(x) = 2sum_(n ge 1)(n!)/((n-1)!1!)x^n`
`A(x) = 2sum_(n ge 1)(n*n!)/(n!)x^n`
`A(x) = 2sum_(n ge 0)(n*n!)/(n!)x^n`
So `color(red)(a_n = 2n(n!))`
8.34: Let `h_0=1`, and let `h_n` be the number of compositions of `n` into parts equal to `2` or `3`. Find a closed formula for `H(x)=sum_(n ge 0)h_nx^n`
Consider removing the `n^(th)` part of the composition
If it was of size `2`, then there are `h_(n-2)` ways to get a composition of `n`
If it was of size `3`, then there are `h_(n-3)` ways to get a composition of `n`
So we get the recurrence `h_n = h_(n-2)+h_(n-3)` for `n ge 3` and `h_0=1, h_1=0, h_2=1`
Multiply the recurrence by `x^n` and sum over all `n ge 3`:
`sum_(n ge 3)h_nx^n = sum_(n ge 3)h_(n-2)x^n + sum_(n ge 3)h_(n-3)x^n`
`H(x)-h_0-h_1x-h_2x^2 = x^2sum_(n ge 3)h_(n-2)x^(n-2) + x^3sum_(n ge 3)h_(n-3)x^(n-3)`
`H(x)-1-x^2 = x^2(H(x)-h_0) + x^3H(x)`
`H(x)-1-x^2 = x^2H(x)-x^2+x^3H(x)`
`H(x)-x^2H(x)-x^3H(x) = 1`
`H(x)(1-x^2-x^3) = 1`
`H(x) = color(red)(1/(1-x^2-x^3))`
Alternatively, since the number of parts are unspecified, we could compose generating functions
Let `h_n` be the number of ways to break up `[n]` into consecutive intervals of sizes `2` and `3`
Let `alpha` be the ways to create a set of size `2` or `3`
So `a_2=a_3=1` and `a_n = 0` for `n != 2,3`
So `A(x) = sum_(n ge 0)a_nx^n = x^2+x^3`
`H(x) = 1/(1-A(x)) = color(red)(1/(1-x^2-x^3))`
8.35: Let `H_n` be the number of ways to tile a `1xxn` rectangle with `1xx1` tiles that are red or blue and `1xx2` tiles that are green, yellow, or white. Find a closed formula for `H(x)=sum_(n ge 0)h_nx^n`
Consider removing the `n^(th)` tile
If it was a `1xx1` tile, then there are `2` ways to create the rectangle
If it was a `1xx2` tile, then there are `3` ways to create the rectangle
So we get the recurrence `h_n = 2h_(n-1)+3h_(n-2)` for `n ge 2` and `h_0=1, h_1=2`
Multiply the recurrence by `x^n` and sum over all `n ge 2`:
`sum_(n ge 2)h_nx^n = sum_(n ge 2)2h_(n-1)x^n + sum_(n ge 2)3h_(n-2)x^n`
`H(x)-h_0-h_1x = 2xsum_(n ge 2)h_(n-1)x^(n-1) + 3x^2sum_(n ge 2)h_(n-2)x^(n-2)`
`H(x)-1-2x = 2x(H(x)-h_0) + 3x^2H(x)`
`H(x)-1-2x = 2xH(x)-2x+3x^2H(x)`
`H(x)-2xH(x)-3x^2H(x) = 1`
`H(x)(1-2x-3x^2) = 1`
`H(x) = color(red)(1/(1-2x-3x^2))`
8.36: Let `h_n` be the number of sequences of length `n` consisting of letters `A` and `B` in which there is no subsequence of two letters `A` in consecutive positions. Find a closed formula for `H(x)=sum_(n ge 0)h_nx^n`
Consider the last letter of the sequence
If it is a `B`, then there are `h_(n-1)` ways to form this sequence
If it is an `A`, then there are `h_(n-2)` ways to form this sequence because the second to last letter must be a `B`
So we get the recurrence `h_n = h_(n-1) + h_(n-2)` where `h_0 = 1` and `h_1 = 2`
Multiply the recurrence by `x_n` and sum over all `n ge 2`:
`sum_(n ge 2)h_nx^n = sum_(n ge 2)h_(n-1)x^n + sum_(n ge 2)h_(n-2)x^n`
`H(x)-h_0-h_1x = xsum_(n ge 2)h_(n-1)x^(n-1) + x^2sum_(n ge 2)h_(n-2)x^(n-2)`
`H(x)-1-2x = x(H(x)-h_0) + x^2H(x)`
`H(x)-1-2x = xH(x)-x + x^2H(x)`
`H(x)-xH(x)-x^2H(x) = 1+x`
`H(x)(1-x-x^2) = 1+x`
`H(x) = color(red)((1+x)/(1-x-x^2))`
8.39: Let `t_n` be the number of ways to arrange `n` books on two bookshelves so that each shelf receives at least one book. Find a closed formula for `t_n`
We want to split up the books into two nonempty subsets and order the books in each subset
Let `a_n` be the number of ways to order the books in the first shelf
Let `b_n` be the number of ways to order the books in the second shelf
`a_n = b_n = {(0\ text(if ) n = 0), (n!\ text(if ) n ge 0):}`
`t_n` is the coefficient of `x^n/(n!)` in the product `A(x)B(x)`
`= (sum_(n ge 0)a_n/(n!)x^n)(sum_(n ge 0)b_n/(n!)x^n)`
`= (sum_(n ge 1)a_n/(n!)x^n)(sum_(n ge 1)b_n/(n!)x^n)`
`= (sum_(n ge 1)(n!)/(n!)x^n)(sum_(n ge 1)(n!)/(n!)x^n)`
`= (sum_(n ge 1)x^n)(sum_(n ge 1)x^n)`
`= (xsum_(n ge 1)x^(n-1))(xsum_(n ge 1)x^(n-1))`
`= (xsum_(n ge 0)x^n)(xsum_(n ge 0)x^n)`
`= (x/(1-x))(x/(1-x))`
`= x^2(1-x)^(-2)`
`= x^2sum_(n ge 0)((-2),(n))(-x)^n`
`= x^2sum_(n ge 0)((n+1),(n))(-1)^n(-1)^nx^n`
`= x^2sum_(n ge 0)(n+1)x^n`
`= sum_(n ge 0)(n+1)x^(n+2)`
`= sum_(n ge 2)(n-1)x^n`
`= sum_(n ge 2)(n!(n-1))/(n!)x^n`
So `color(red)(t_n = n!(n-1))` for `n ge 2` and `color(red)(t_0 = t_1 = 0)`
8.43: We divide a group of people into subgroups `A`, `B`, and `C`, and ask each subgroup to form a line. We also require that `A` have an odd number of people, and that `B` have an even number of people. How many ways are there to do this?
Let `a_n` be the number of ways to order the people in `A` in a line
Let `b_n` be the number of ways to order the people in `B` in a line
Let `c_n` be the number of ways to order the people in `C` in a line
`a_n = {(n! text( if ) n text( odd)),(0 text( if ) n text( even)):}`
`b_n = {(n! text( if ) n text( even)),(0 text( if ) n text( odd)):}`
`c_n = n!`
The answer is the coefficient of `x^n/(n!)` in the product `A(x)B(x)C(x)`
`=(sum_(n ge 0)a_n/(n!)x^n)(sum_(n ge 0)c_n/(n!)x^n)(sum_(n ge 0)c_n/(n!)x^n)`
`=(sum_(n text( odd ))(n!)/(n!)x^n)(sum_(n text( even ))(n!)/(n!)x^n)(sum_(n ge 0)(n!)/(n!)x^n)`
`=(sum_(n text( odd ))x^n)(sum_(n text( even ))x^n)(sum_(n ge 0)x^n)`
`=(sum_(n ge 0)x^(2n+1))(sum_(n ge 0)x^(2n))(sum_(n ge 0)x^n)`
`=(xsum_(n ge 0)x^(2n))(sum_(n ge 0)x^(2n))(sum_(n ge 0)x^n)`
`=(x/(1-x^2))(1/(1-x^2))(1/(1-x))`
And use partial fraction decomposition to continue
8.44: We select an odd number of people from a group of `n` people to serve on a committee. Then we select an even number from this committee to serve on a subcommittee. In how many different ways can we do this?
This is the same problem as picking subsets `A sube B sube [n]` such that `A` is even, `B\\A` is odd, and `[n]\\B` can be even or odd
(We frame the problem this way to set the problem up with disjoint sets whose union is the whole set)
Let `a_n` be the number of ways for a subset to be even
Let `b_n` be the number of ways for a subset to be odd
Let `c_n` be the number of ways for a subset to be of size `n`
`a_n = {(1 text( if ) n text( even)), (0 text( if ) n text( odd)):}`
`b_n = {(1 text( if ) n text( odd)), (0 text( if ) n text( even)):}`
`c_n = 1`
The answer is the coefficient of `x^n/(n!)` in the product `A(x)B(x)C(x)`
`= (sum_(n ge 0)a_n/(n!)x^n)(sum_(n ge 0)b_n/(n!)x^n)(sum_(n ge 0)c_n/(n!)x^n)`
`= (sum_(n text( even))1/(n!)x^n)(sum_(n text( odd))1/(n!)x^n)(sum_(n ge 0)1/(n!)x^n)`
`= ((e^x+e^(-x))/2)((e^x-e^(-x))/2)(e^x)`
`= ((e^(2x)-e^(-2x))/4)e^x`
`= 1/4(e^(3x)-e^(-x))`
`= 1/4(sum_(n ge 0)1/(n!)(3x)^n - sum_(n ge 0)1/(n!)(-x)^n)`
`= 1/4(sum_(n ge 0)1/(n!)3^nx^n - sum_(n ge 0)1/(n!)(-1)^nx^n)`
The coefficient of `x^n/(n!)` is `color(red)(1/4(3^n-(-1)^n))`
8.45: We have `n` cards. We want to split them into an even number of non-empty subsets, form a line within each subset, then arrange the subsets in a line. In how many different ways can we do this?
Let `a_n` be the number of ways to form a line of cards
Let `b_n` be the number of ways to form a line of subsets
Let `c_n` be the answer to the problem
`a_n = {(0 text( if ) n = 0),(n! text( if ) n gt 0):}`
`b_n = {(0 text( if ) n text ( odd)),(n! text( if ) n text( even)):}`
So the exponential generating functions are
`A(x) = sum_(n ge 0)a_n/(n!)x^n = sum_(n ge 1)x^n = x/(1-x)`
`B(x) = sum_(n ge 0)b_n/(n!)x^n = sum_(n ge 0)x^2n = 1/(1-x^2)`
The answer is the coefficient of `x^n/(n!)` in the composition `B(A(x))`
`= 1/(1-(x/(1-x))^2)`
`= (1-x)^2/((1-x)^2-x^2)`
`= (1-2x+x^2)/(1-2x)`
`= 1 + x^2/(1-2x)`
`= 1 + x^2sum_(n ge 0)(-2x)^n`
`= 1 + x^2sum_(n ge 0)(-2)^nx^n`
`= 1 + sum_(n ge 0)(-2)^nx^(n+2)`
`= 1 + sum_(n ge 2)(-2)^(n-2)x^n`
`= 1 + sum_(n ge 2)n!(-2)^(n-2)x^n/(n!)`
So `c_n = color(red)(n!(-2)^(n-2))` for `n ge 2`
`c_0` is the constant term, which is `1`
`c_1` is the linear term, which is `0`
8.49:
(a) Let `a_1,a_2,...,a_k` be nonnegative integers, and let `a(n)` be the number of compositions of `n` into `k` parts so that the `i^(th)` part is not larger than `a_i`. Find the ordinary generating function `A(x)=sum_(n ge 0)a(n)x^n`
(b) Let `b(n)` be the number of compositions of `n` into `k+1` parts so that the `i^(th)` part is not larger than `a_i`, and there is no constraint on the last part. Find the ordinary generating function `B(x) = sum_(n ge 0)b(n)x^n`
Since the number of parts is specified, this problem involves multiplying generating functions
(a) This problem is the same as splitting up `[n]` into `k` consecutive intervals such that the `i^(th)` interval has size `ge 1` and `le a_i`
So `A(x) = A_1(x)A_2(x)...A_k(x)` where `A_i(x)` encodes the conditions on the `i^(th)` interval
`A_i(x) = x + x^2 + ... + x^(a_i) = x(1+x+...+x^(a_i-1))`
So `A(x) = prod_(i=1)^k x(1+x+...+x^(a_i-1)) = color(red)(prod_(i=1)^k x(1-x^(a_i))/(1-x))`
(b) With the same constraints on `1 le i le k`, we have
`B(x) = A_1(x)A_2(x)...A_k(x)A_(k+1)(x)`
Since there is no constraint for the `(k+1)^(st)` part, we have
`A_(k+1) = x + x^2 + ... = x(1 + x + x^2 + ...) = x1/(1-x)`
So `B(x) = color(red)((xA(x))/(1-x))`
Chapter 7
7.3: How many positive integers `k le 210` are relatively prime to `210`?
We can count the number of integers that are not relatively prime to `210` and subtract that from `210`
An integer is not relatively prime to `210` if it is divisible by `2` or `3` or `5` or `7`
Let `A_2` be the set of integers divisible by `2`
Let `A_3` be the set of integers divisible by `3`
Let `A_5` be the set of integers divisible by `5`
Let `A_7` be the set of integers divisible by `7`
Then the set of all integers relatively prime to `210` are in the union `A_2 uu A_3 uu A_5 uu A_7`
By inclusion-exclusion, `|A_2 uu A_3 uu A_5 uu A_7|`
`= |A_2| + |A_3| + |A_5| + |A_7|`
`- |A_2 nn A_3| - |A_2 nn A_5| - |A_2 nn A_7| - |A_3 nn A_5| - |A_3 nn A_7| - |A_5 nn A_7|`
`+ |A_2 nn A_3 nn A_5| + |A_2 nn A_3 nn A_7| + |A_2 nn A_5 nn A_7| + |A_3 nn A_5 nn A_7|`
`- |A_2 nn A_3 nn A_5 nn A_7|`
There are `210/2 = 105` integers divisible by `2`, so `|A_2| = 105`
There are `210/(2*3) = 35` integers divisible by `2` and `3`, so `|A_2 nn A_3| = 35`
(A number divisible by `2` and `3` is divisible by `6`)
There are `210/(2*3*5) = 7` integers divisible by `2` and `3` and `5`, so `|A_2 nn A_3 nn A_5| = 7`
So the number of integers not relatively prime to `210` is
`105+70+42+30-35-21-15-14-10-6+7+5+3+2-1 = 162`
The number of integers relatively prime to `210` is
`210-162 = color(red)(48)`
7.4: Let `m` be a positive integer. Denote by `phi(m)` the number of integers in `[m]` that are relatively prime to `m`. Let `p,q,r` be distinct prime numbers. Compute `phi(pqr)`
We can count the number of integers that are not relatively prime to `pqr` and subtract that from `pqr`
An integer is not relatively prime to `pqr` if it is divisible by `p` or `q` or `r`
Let `A_p` be the set of integers divisible by `p`
Let `A_q` be the set of integers divisible by `q`
Let `A_r` be the set of integers divisible by `r`
Then the set of all integers relatively prime to `pqr` are in the union `A_p uu A_q uu A_r`
By inclusion-exclusion, `|A_p uu A_q uu A_r|`
`= |A_p| + |A_q| + |A_r| - |A_p nn A_q| - |A_p nn A_r| - |A_q nn A_r| + |A_p nn A_q nn A_r|`
`= qr + pr + pq - r - q - p + 1`
which is the number of integers not relatively prime to `pqr`
So the number of integers relatively prime to `pqr` is
`color(red)(pqr - qr - pr - pq + r + q + p - 1) = (p-1)(q-1)(r-1)`
7.13: Let `p = p_1p_2...p_n` be an `n`-permutation, and assume `n ge 3`. `i` is an excedence of `p` if `p_i gt i`. Compute the number of `n`-permutations whose excedence set contains at least one of `n-2` and `n-1`
Let `A_(n-1)` be the set of `n`-permutations whose excedence set contains only `n-1`
Let `A_(n-2)` be the set of `n`-permutations whose excedence set contains only `n-2`
Then the number of `n`-permutations whose excedence set contains at least one of `n-2` and `n-1` is the union `A_(n-1) uu A_(n-2)`
By inclusion-exclusion, `|A_(n-1) uu A_(n-2)|`
`= |A_(n-1)| + |A_(n-2)| - |A_(n-1) nn A_(n-2)|`
For `n-1` to be an excedence, the number at the `(n-1)^(st)` spot has to be bigger than `n-1`. There is only one number (`n`) bigger than `n-1`, so there is only one choice for `p_(n-1)`. There are `n-1` remaining numbers for the rest of the spots, so `|A_(n-1)| = (n-1)!`
For `n-2` to be an excedence, the number at the `(n-2)^(nd)` spot has to be bigger than `n-2`. There are two numbers (`n` and `n-1`) bigger than `n-2`, so there are two choices for `p_(n-2)`. There are `n-1` remaining numbers for the rest of the spots, so `|A_(n-2)| = 2(n-1)!`
For `n-1` and `n-2` to be an excedence, the number at the `(n-1)^(th)` spot has to be bigger than `n-1` and the number at the `(n-2)^(nd)` spot has to be bigger than `n-2`. `p_(n-1)` is forced to be `n`, which forces `p_(n-2)` to be `n-1`. There are `n-2` remaining numbers for the rest of the spots, so `|A_(n-1) nn A_(n-2)| = (n-2)!`
So the number of `n`-permutations whose excedence set contains at least one of `n-2` and `n-1` is
`(n-1)! + 2(n-1)! - (n-2)!`
`= color(red)(3(n-1)! - (n-2)!)`
7.15: How many partitions of `[n]` contain at least one of the singleton blocks `{1}` and `{n}`?
Let `A_1` be the set of partitions containing the singleton block `{1}`
Let `A_n` be the set of partitions containing the singleton block `{n}`
The set of partitions containing at least one of the singleton blocks is the union `A_1 uu A_n`
By inclusion-exclusion, `|A_1 uu A_n|`
`= |A_1| + |A_n| - |A_1 nn A_n|`
For `A_1`, we put `1` in its own block. Then there are `n-1` numbers to put into blocks, which is counted by `B(n-1)`
For `A_1 nn A_n`, we put `1` and `n` in their own blocks. Then there `n-2` numbers to put into blocks, which is counted by `B(n-2)`
So the number of partitions that contain at least one of the singleton blocks `{1}` and `{n}` is
`B(n-1) + B(n-1) - B(n-2)`
`= color(red)(2B(n-1) - B(n-2))`
7.17: How many compositions does `n` have in which neither the first nor the last entry is `1`?
Count the number of compositions that have a `1` in the first entry or a `1` in the last entry and subtract from the total number of compositions
Let `A_1` be the set of compositions that have a `1` in the first entry
Let `A_2` be the set of compositions that have a `1` in the last entry
Then the set of compositions in which the first or last entry is a `1` is the union `A_1 uu A_2`
By inclusion-exclusion, `|A_1 uu A_2|`
`= |A_1| + |A_2| - |A_1 nn A_2|`
For `A_1`, since there is a `1` in the first entry, the problem turns into compositions of `n-1`, of which there are `2^(n-1-1) = 2^(n-2)`
For `A_1 nn A_2`, since there is are `1`'s in the first and last entry, the problem turns into compositions of `n-2`, of which there are `2^(n-2-1) = 2^(n-3)`
So the number of compositions in which the first or last entry is a `1` is
`2^(n-2) + 2^(n-2) - 2^(n-3)`
`= 2*2^(n-2) - 2^(n-3)`
`= 2^(n-1) - 2^(n-3)`
The number of compositions in which neither the first nor last entry is `1` is
`2^(n-1) - 2^(n-1) + 2^(n-3)`
`= color(red)(2^(n-3))`
7.20: Let `D(n)` be the number of derangements of a set of size `n`. Give a combinatorial proof of the identity `D(n+1) = n(D(n)+D(n-1))` for `n ge 1`
Consider the set `[n+1]`
Consider the number `n+1`. There are `n` choices for it
Suppose `n+1` is mapped to `i`
If `i` is not mapped to `n+1`, then we are now looking at derangements of a set of size `n`, which is `D(n)`
If `i` is mapped to `n+1`, then we are now looking at derangements of a set of size `n-1`, which is `D(n-1)`
So the number of derangements for a set of size `n+1` is `n(D(n)+D(n-1))`
7.24: How many three-digit positive integers are divisible by at least one of six and seven?
Let `A_6` be the set of integers divisible by six
Let `A_7` be the set of integers divisible by seven
Then the set of integers divisible by six or seven is the union `A_6 uu A_7`
By inclusion-exclusion, `|A_6 uu A_7|`
`= |A_6| + |A_7| - |A_6 nn A_7|`
There are `900/6 = 150` integers divisible by six, so `|A_6| = 150`
There are `lfloor900/7rfloor = 128` integers divisible by seven, so `|A_7| = 128`
There are `lfloor900/42rfloor = 21` integers divisible by six and seven, so `|A_6 nn A_7| = 21`
So the number of integers divisible by at least one of six and seven is
`150 + 128 - 21 = color(red)(257)`
7.25: How many two-digit positive integers are relatively prime to both two and three?
Count the number of integers not relatively prime to two or three and subtract from the total number of two-digit positive integers
Let `A_2` be the set of integers divisible by two
Let `A_3` be the set of integers divisible by three
Then the set of integers divisible by two or three is the union `A_2 uu A_3`
By inclusion-exclusion, `|A_2 uu A_3|`
`= |A_2| + |A_3| - |A_2 nn A_3|`
There are `90/2 = 45` integers divisible by two, so `|A_2| = 45`
There are `90/3 = 30` integers divisible by three, so `|A_3| = 30`
There are `90/6 = 15` integers divisible by two and three, so `|A_2 nn A_3| = 15`
So the number of integers divisible by two or three is
`45 + 30 - 15 = 60`
The number of two-digit positive integers that are relatively prime to both two and three is
`90 - 60 = color(red)(30)`
7.26: In how many ways can we list the digits `{1,1,2,2,3,4,5}` so that two identical digits are not in consecutive positions?
Count the number of arrangements that have consecutive `1`'s or consecutive `2`'s and subtract from the total number of arrangements
Let `A_1` be the set of arrangements that have consecutive `1`'s
Let `A_2` be the set of arrangements that have consecutive `2`'s
Then the set of arrangements that have consecutive `1`'s or consecutive `2`'s is the union `A_1 uu A_2`
By inclusion-exclusion, `|A_1 uu A_2|`
`= |A_1| + |A_2| - |A_1 nn A_2|`
We can combine the two `1`'s into one `1` since they have to go together
Then there are `(6!)/(2!)` ways to arrange the numbers, so `|A_1| = (6!)/(2!)
We can also combine the two `2`'s into one `2` since they have to go together
Then there are `5!` ways to arrange the numbers, so `|A_1 nn A_2| = 5!`
So the number of arrangements that have consecutive `1`'s or consecutive `2`'s is
`(6!)/(2!) + (6!)/(2!) - 5!`
`= 2(6!)/(2!) - 5!`
`= 6! - 5!`
The number of arrangements that don't have consecutive `1`'s and `2`'s is
`color(red)(7! - 6! + 5!)`
7.27: How many positive integers are there that are not larger than `1000` and are neither perfect squares nor perfect cubes?
Count the number of integers that are perfect squares or perfect cubes and subtract from the total number of integers
Let `A_2` be the set of perfect squares
Let `A_3` be the set of perfect cubes
Then the set of perfect squares or perfect cubes is the union `|A_2 uu A_3|`
By inclusion-exclusion, `|A_2 uu A_3|`
`= |A_2| + |A_3| - |A_2 nn A_3|`
There are `lfloorsqrt(1000)rfloor = 31` perfect squares, so `|A_2| = 31`
There are `root(3)(1000) = 10` perfect cubes, so `|A_3| = 10`
A perfect square that is also a perfect cube is a number that has the form `(x^2)^3 = x^6`
There are `lfloorroot(6)(1000)rfloor = 3` numbers that are perfect squares and perfect cubes
So the number of integers that are perfect squares or perfect cubes is
`31 + 10 - 3 = 38`
The number of integers that are neither perfect squares nor perfect cubes is
`1000 - 38 = color(red)(962)`